Coursera機械学習の第6週では、実際に機械学習を使う時に、いかに時間を無駄にしないで良いモデルを作成するかについて説明しております。
実際に業務で機械学習を使って分析をしていたので、知っている事も多かったですが、「なるほど！それを知っていればもう少し上手くできたのに・・」という内容もありました。
本記事では、第６週の前半の「機械学習適用時のアドバイス」について記載します。
どうすればモデルを改善できるか？
機械学習でモデルを作成したけど思ったほど精度が出なかった場合、何をすれば良いのでしょうか？
- 教師データの数を増やす
- 特徴量の数を増やす
- 特徴量の数を減らす
- 特徴量を組み合わせて新しい特徴量を作る
- 正則化パラメータ($\lambda$)を大きくする
- 正則化パラメータ($\lambda$)を小さくする
などなどの対策が思いつきますが、特徴量を増やすのはどういう場合で、減らすのはどういう場合でしょうか？
まず前提として、モデルの性能は学習に使用していないテストデータによって評価します。
手持ちのデータをモデルの生成のために使用する教師データと、モデルを評価するためのテストデータに分ける事になります。
ただし、ここに大きな罠があります。
以下の単回帰モデルで最適な多項式の次数$d$の値はいくつになるか・・
$$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 + \cdots + \theta_dx^d$$
実際にモデルを作成してみないとわからないので$d$を$1,2,3 \cdots$と変えてモデルを作成したとします。(上記の「特徴量を組み合わせて新しい特徴量を作る」の最も機械的な方法となります。）
このとき、それぞれのモデルでテストデータの目的関数を計算したら$d=3$の時に値が最少になったとします。（図で表すと以下のようになります。）
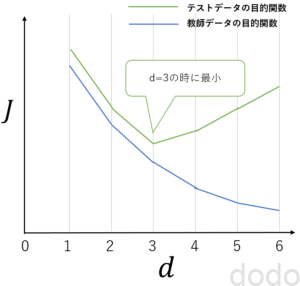（例）目的関数と多項式の次数目的関数が最小ということは最も精度が良いということなので、最適な次数は$d=3$となりました！
・・・というのはダメです。
何故ならば、次数を決めるため・・つまりモデルを作成するために、テストデータを使っているからです。
テストデータを見て学習しているのと同じ事になります。
ではどうすれば良いのでしょうか？
本講座では、データを「教師データ」「検証データ」「テストデータ」の３つに分ける事を強く推奨しております。
講座では、Cross Validation(交差検証）データという言葉を使ってますが・・この言葉はちょっと誤解を招きます。通常、交差検証は、教師データと検証データの分け方を数パターン試す場合に使用します。（フォーラムでも指摘されております。）
なので、本記事では、交差検証データではなく、検証データと記載します。
モデルの作成は、教師データと検証データで行い、多項式の次数$d$は検証データの目的関数が最小になる値を選択します。
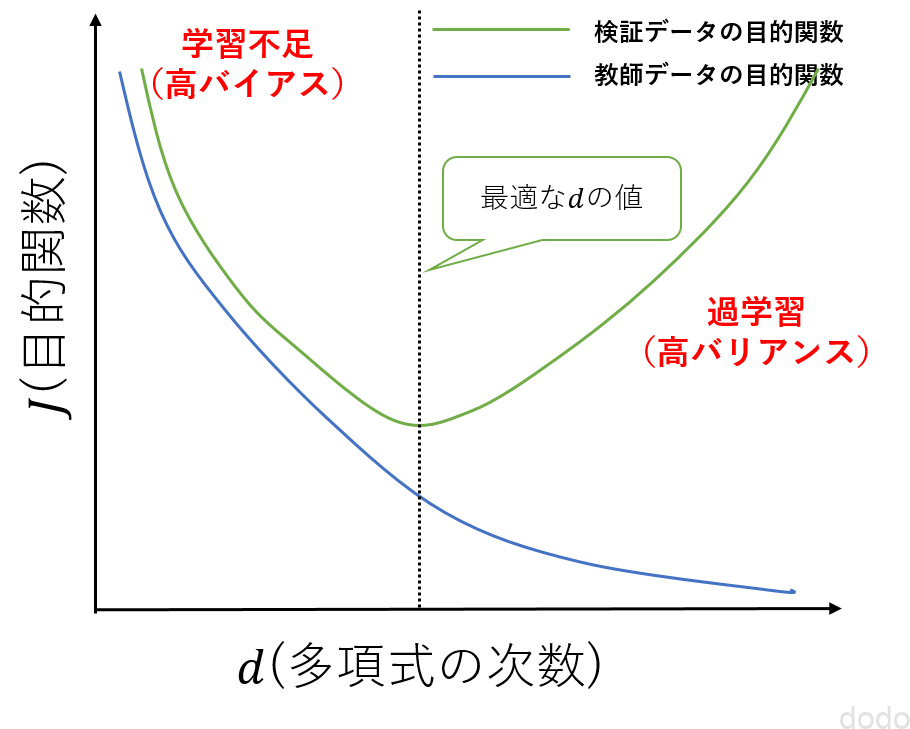目的関数と多項式の次数の関係なお、多項式の次数が小さすぎると教師データも検証データも精度が悪い状態（高バイアス）、多項式の次数が大きすぎると教師データの精度だけ良くて検証データの精度が悪い状態（高バリアンス）になります。
つまり、高バイアスならば多項式の次数を増やして、高バリアンすならば多項式の次数を減らしていくという事になります。
そして最終的にテストデータによりモデルを評価します。
過去の実業務では、検証データ＝テストデータとしていました。
しかしそれだと結局、そのモデルを本当に評価するためには、別途データが必要になってしまいます。
最初から３つに分ければ良かったのですね・・
上記は多項式の次元を増やす（特量量を組み合わせて新しい特徴量を作る）場合の例でしたが、「特徴量を増やす/減らす」場合も同様の傾向、つまり特徴量の数が多いほど高バリアンス、少ないほど高バイアスの傾向を示します。
「どの特徴量を選択するか」といった課題もありますが、例えば高バリアンスならば特徴量の数を減らすといった対処が有効になります。
なお、正則化のパラメータ$\lambda$を変化させた場合は、目的関数との関係は以下の図のようになります。
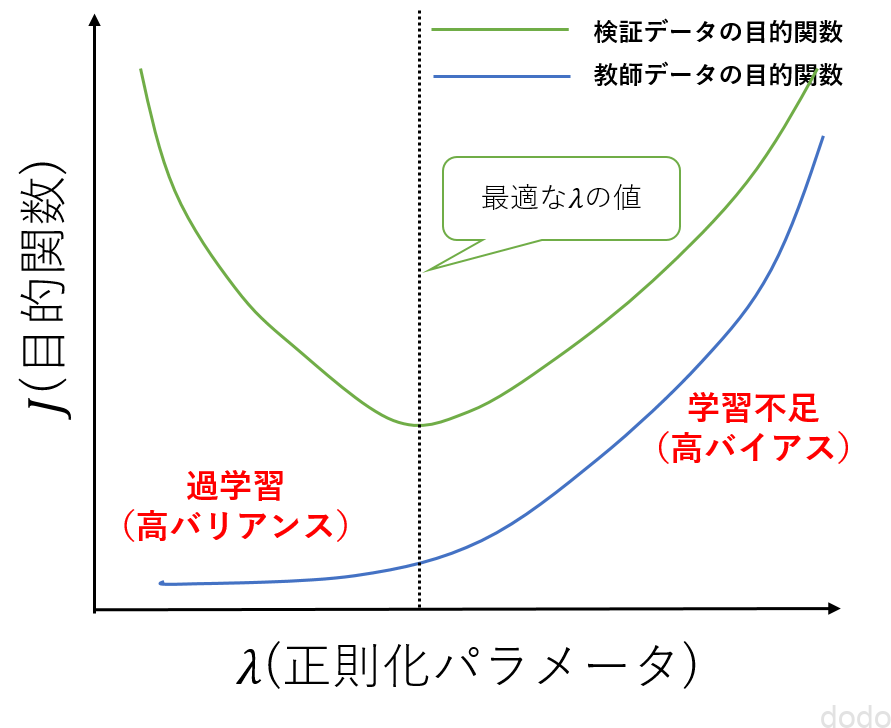目的関数と正則化パラメータの関係この場合も$\lambda$を変化させていき検証データの目的関数が最小になる場合の$\lambda$を選択します。
学習曲線
特徴量と$\lambda$については、検証データの目的関数を求めて、その関係性から最適な値を選べば良いことがわかりました。
では、教師データの数についてはどうでしょうか？
単純に考えると、教師データは多ければ多いほど良さそうに思います。
ただし「苦労してかき集めて増やしてもモデルの性能は大きく改善しないので、それよりももっと他にやることがあるだろ！」というケースがあります。
それはバイアスが高い場合です。
以下のグラフは、単回帰のモデルを作成するためにデータを増やしていった場合のイメージです。
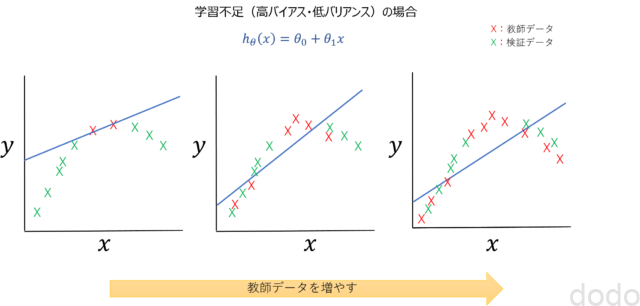高バイアスで教師データを増やした場合教師データの数が少ない時は教師データに対する精度は高いですが（データが少ないのでフィットしやすい）、検証データには全くフィットしていません。
そこで、教師データの数を増やしていくと検証データにもある程度はフィットするようになりますが、それでもモデルが単純すぎるため限界があります。
逆にバリアンスが高い場合は、以下のように学習データを増やすほど過学習が抑えられるため、データを増やす事によって精度の改善が見込まれます。
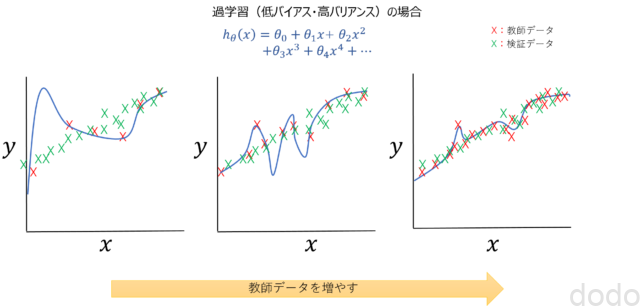高バリアンスで教師データを増やした場合この現象を目的関数と教師データ数のグラフで表現すると以下のようになります。（このグラフを学習曲線と言います。）
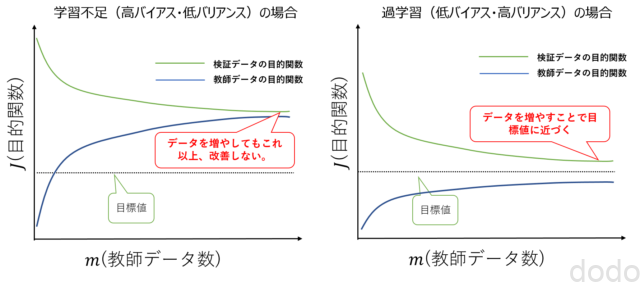学習曲線バイアスが高い場合は教師データと検証データの目的関数の値はほぼ同じ値に収束するため、教師データの目的関数の値が目標値よりも高い場合、いくら頑張って教師データを増やしても、目標値に達する事はありません。
やるべきことはモデルの改善です。
どうすればモデルを改善できるか？・・のまとめ
以上、まとめると、以下のようになります。
- 教師データを追加する。
- 特徴量を減らす。
- $\lambda$の値を大きくする。
- 特徴量を追加する。
- 多項式の次数を上げる。
- $\lambda$の値を小さくする。
なお講座では、ニューラルネットワークの場合についても言及されており、階層が少ないとバイアスが高く、階層が多いとバリアンスが高い傾向になると言ってます。
ただし、一般的には、計算コストを度外視すれば、階層は多い方がよく、過学習する場合（バリアンすが高い場合）は、階層を少なくするよりも正則化をした方が良いと言及されてます。
また１つの階層のユニット数については、多項式の次数や$\lambda$のように検証データを用いて最も最適な数を選ぶのが良いとのことです。
まとめ
講座では、ここで説明した事を理解すれば、そんじょそこらのシリコンバレーで働いている人よりも、効率的に仕事できる・・と言ってますが、ちょっと言い過ぎだと思います・・
ただ以下の２点については、非常に勉強になりました。
- データを教師データ・検証データ・テストデータの３つに分ける事
- バイアスが高い状態で教師データを頑張って増やしても意味ない事
次回は第6週の後半について受講記を記載していきます。
