Coursera「機械学習」の第4週は、いよいよニューラルネットワークです。
ニューラルネットワークになると、ちょっと一般の人が想像するA.I.っぽくなりますね。
Coursera「機械学習」ではニューラルネットワークについて2週（4週と5週目）に渡って説明されております。
本記事では、第４週で学習するニューラルネットワークのモデルとしての表現についてまとめております。
非線形モデルについて
ロジスティック回帰は線形モデルですが、多項式として非線形の項目を追加すれば（教師データを加工して特徴量として追加する）、非線形なモデルも扱う事もできます。
\begin{align*}& g(\theta_0 + \theta_1x_1^2 + \theta_2x_1x_2 + \theta_3x_1x_3 + \theta_4x_2^2 + \theta_5x_2x_3 + \theta_6x_3^2 )\end{align*}
なので、いくらでも複雑なモデルが作れるので、ニューラルネットワークとか使わなくても事足りるように感じますが、実際に多項式を導入しようとすると、特徴量の数が爆発的に増えてしまい計算できなくなります。
例えば、100×100(px)の画像（グレイスケール）のデータから何かを判別しようとした場合、元の特徴量の数だけでも100×100=10,000個となり、$x_1^2$、$x_1x_2$などの2乗項まで取り入れただけでも${}_{10000} \mathrm{ H }_2=50005000$で約5千万個の特徴量となって、とても計算できたものではありません・・(因みに３乗項まで入れると１０００億の桁になります・・）
このような背景から、特徴量が多く非線形なモデルを扱う手法としてニューラルネットワークが登場します。
ニューラルネットワークと脳
ニューラルネットワークの名称は脳の神経細胞の処理との類似から来ています。
脳は、以下の図のように神経細胞が、いくつも連結して情報の入出力処理を実行してます。
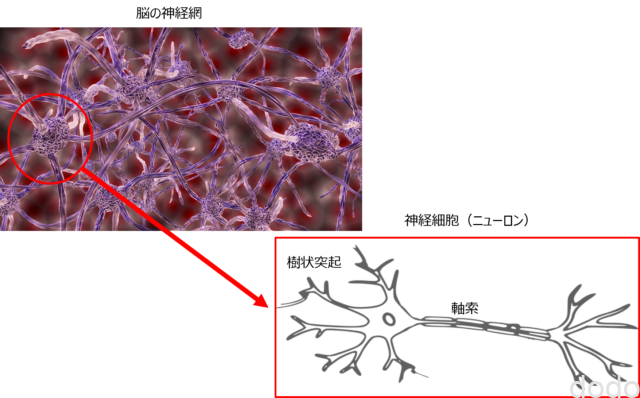脳と神経細胞ここで、１つの神経細胞の入出力は、ロジスティック回帰の入出力モデルと類似しています。
樹状突起から入ってきた入力情報が細胞体によって活性化され、軸索に出力されますが、この処理は、入力情報$x$がシグモイド関数$g$によって活性化されて（このことから一般的に活性化関数とも言います。）$h(\theta)$として出力されるロジスティック回帰でモデル化できます。
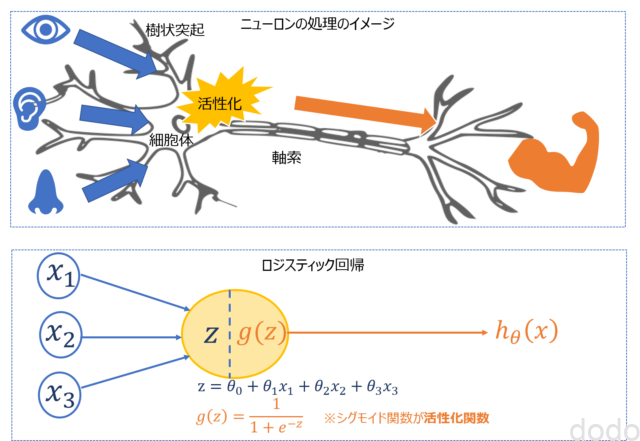神経細胞とロジスティック回帰この事から、複雑な脳神経網は、ロジスティック回帰モデルのような「入力を活性化関数によって変換して出力するようなモデル」を「複数連結させて入出力を行うようなモデル」で表現できます。
このようなモデルをニューラルネットワークと言います。
ニューラルネットワークの数式表現
ロジスティック回帰では入力層（ユニット（図の中で◯で表現）の数は特徴量の数）と出力層（ユニットの数は２分類では１つ）だけだったのが、ニューラルネットワークでは、入力層と出力層の間に隠れ層が存在します。
以下の図は、隠れ層が２つ（合計４層）で、第２層のユニット数が３つ、第3層のユニット数が4つの例です。
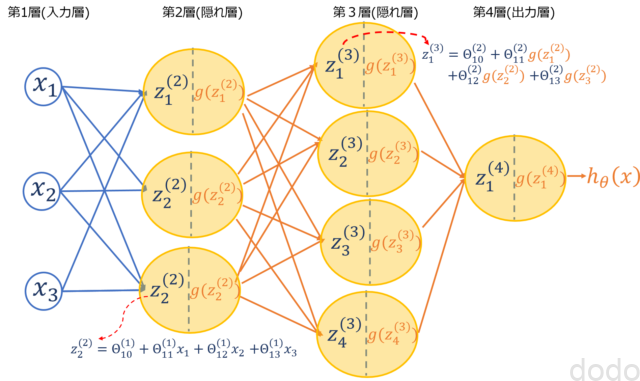ニューラルネットワーク（４層）の例ロジスティック回帰は、以下のような数式で表すことができました。
\begin{align}
z&=\theta^Tx \\
h_\theta(x)&=g(z) \\
\end{align}
ここで、$x$、$\theta$は以下で定義されます。
\begin{align}
x&=\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n \end{bmatrix} \qquad (n:\text{特徴量の数},x_0=1)\\
\theta&=\begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix} \qquad (n:\text{特徴量の数})
\end{align}
それに対して上の図の例の４層のニューラルネットワークは、以下のような数式で表すことができます。
\begin{align}
z^{(2)} &= \Theta^{(1)}x \\
z^{(3)} &= \Theta^{(2)}g(z^{(2)}) \\
z^{(4)} &= \Theta^{(3)}g(z^{(3)}) \\
h_\Theta(x)&=g(z^{(4)}) \\
\end{align}
ここで、$x$、$\Theta^{(l)}$、$g(z^{(l)})$は以下で定義されます。
\begin{align}
x&=\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n \end{bmatrix} \qquad (n:\text{特徴量の数},x_0=1)\\
\Theta^{(j)}&= \left( \begin{array}{cccc} \Theta^{(j)}_{ 11 } & \Theta^{(j)}_{ 12 } & \ldots & \Theta^{(j)}_{ 1s_j+1 } \\ \Theta^{(j)}_{ 21 } & \Theta^{(j)}_{ 22 } & \ldots & \Theta^{(j)}_{ 2s_j+1 } \\ \vdots & \vdots & \ddots & \vdots \\ \Theta^{(j)}_{ s_{(j+1)}1 } & \Theta^{(j)}_{ s_{(j+1)}2 } & \ldots & \Theta^{(j)}_{ s_{(j+1)}s_j +1 } \end{array} \right) \qquad (j:\text{層番号},s_j:\text{第j層のユニット数})\\
g(z^{(j)})&=\begin{bmatrix} 1 \\ g(z_1^{(j)}) \\ \vdots \\ \ g(z_{s_j}^{(j)})\end{bmatrix} \qquad (j:\text{層番号},s_j:\text{第j層のユニット数})
\end{align}
さらに$a_i^{(j)}=g(z_i^{(j)})$を導入し、$x_i=a_i^{(1)}$とすることにより、一般的に以下のように表すことができます。
\begin{align}
z^{(j+1)} &= \Theta^{(j)}a^{(j)} \qquad (j:\text{層番号})\\
h_\Theta(x) &= a^{(J)}\qquad (J:\text{出力層の番号})\\
\end{align}
ここで$a^{(j)}$は以下で定義されます。
\begin{align}
a^{(j)}&=\begin{bmatrix} a_0^{(j)} \\ a_1^{(j)} \\ \vdots \\ \ a_{s_j}^{(j)}\end{bmatrix} \qquad (j:\text{層番号},s_j:\text{第j層のユニット数},a_0^{(j)}=1)
\end{align}
なお$j=1$(入力層)の場合は、$s_1$(第1層のユニット数)は特徴量の数です。
多クラス分類
２分類では、出力層のユニット数は１つですが、３以上の多クラス分類では、出力層のユニット数は、分類するクラスの数となります。
なので$h_\Theta(x)$は２分類では、スカラー値になりますが、多クラス分類では、行数がクラス数の行ベクトルです。（以下のようなイメージです。）
\begin{align}\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline\cdots \newline x_n\end{bmatrix} \rightarrow\begin{bmatrix}a_0^{(2)} \newline a_1^{(2)} \newline a_2^{(2)} \newline\cdots\end{bmatrix} \rightarrow\begin{bmatrix}a_0^{(3)} \newline a_1^{(3)} \newline a_2^{(3)} \newline\cdots\end{bmatrix} \rightarrow \cdots \rightarrow\begin{bmatrix}h_\Theta(x)_1 \newline h_\Theta(x)_2 \newline h_\Theta(x)_3 \newline h_\Theta(x)_4 \newline\end{bmatrix} \end{align}
まとめ
講座では、XNOR回路の入出力が隠れ層を導入することにより実現できる例が紹介されておりますが、省略します。（きっとあっちこっちに載ってます・・）
ここまでは、ロジスティック回帰のモデルが複数組み合わさったようなイメージなので、それを表現するための添字と行列表現がややこしくなったかな・・くらいの印象です。
問題は、この後ですね・・
ロジスティック回帰の目的が$h_\theta(x)$を求める事だったように、ニューラルネットワークでは、$h_\Theta(x)$を求める事になります。
一口に$h_\Theta(x)$と書きましたが、ロジスティック回帰で行ベクトルだったものが各階層毎の行列になるため、求めるべき値が爆発的に増えます。
講座の第5週では、その求め方について学ぶので、次回はそれについての受講記を記載します。
