機械学習

重要度は信用できるか？Permutation Feature Importance(PFI)を試してみた。

  /
mdi-pfi-shap比較

「性能が良いのはわかった。でも理由が知りたい。」

機械学習においてモデルの説明性が求められる事は多いです。

「何故かわからないけど、当たればいいじゃん」というノリでどんどん中身がブラックボックス化して複雑になっていったのに、今更、説明責任が生じるとは理不尽きわまりないですが、やはり理由がわからなければ、危なっかしくて使えないと思うのもわかります。

前回、そのような需要からSHAPという手法について説明しました。

pycarat-error
【説明可能性】PyCarat+SHAPで特徴量の寄与度を可視化してみた。説明可能なAIというような言葉が出てきてから、もう数年が経過しているかと思います。 実際、顧客に「予測の精度が良い」という結果だけ...

SHAPは個別のデータに対する特徴量の寄与度が求められ、可視化したときの見た目も良く、顧客にも説明しやすいです。

一方、計算コストが高い（データが多いほど高くなる）事や、理論的には複雑なので、細かいロジックを知りたがる顧客には、逆に説明しにくいなどの欠点もあります。

とはいえ、scikit-learnの分類器のデフォルトの重要度だと物足りない・・というかデータによっては、かなりバイアスがかかった結果になる場合があるのです。

そんな中、Permutation Feature Importance(PFI)という重要度が、近年よく使われています。

本記事では、デフォルトの重要度、PFI、SHAPでそれぞれ重要度（寄与度）を計算して比較してみます。

Permutation Feature Importance(PFI)とは？

Permutation Feature Importance(PFI)の手法は単純です。

元のデータと、ある特徴量の値を完全にシャッフルしたデータで、それぞれの正解データと予測データの誤差を比較して、その差を特徴量の重要度とします。

つまり、シャッフルした事により結果が悪くなれば（誤差が大きくなれば）その特徴量は重要、シャッフルしても結果に影響なければその特徴量は重要でないということになります。

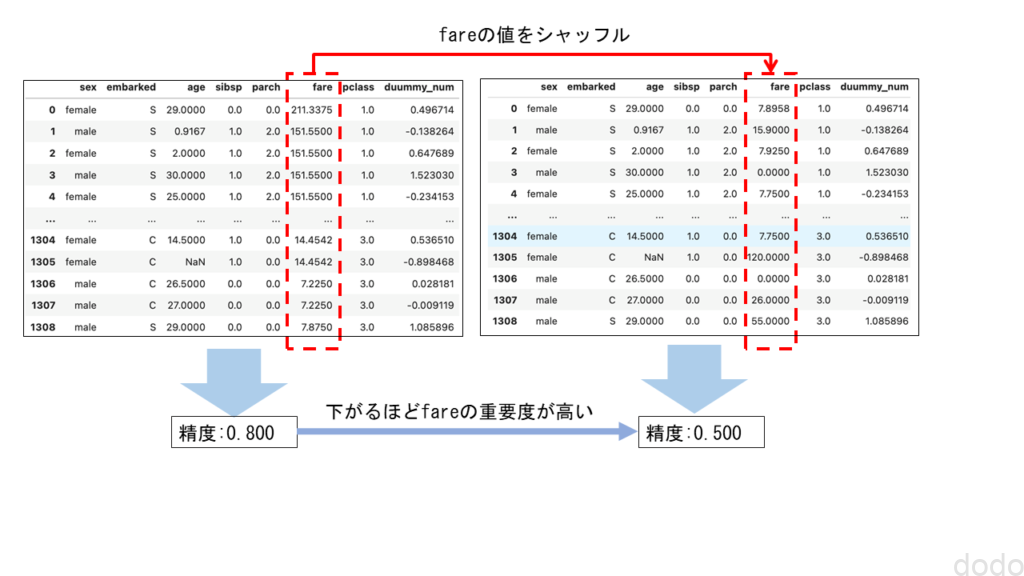PFIイメージPFIイメージ

PFIの大きな利点は、以下の２つになります。

  1. モデルのアルゴリズムに依存しない。
    入力データを変えて比較するだけなので、アルゴリズムに依存せずどんなモデルにも適用できます。
  2. 計算コストが低い。
    上記のロジックを見て「そんな事をしないで、その特徴量をデータから削除して比較すれば良いのでは？」と思った方もいられるかもしれません。
    しかし、特徴量を削除するということはモデルを作成し直すという事なのでコストがかかります。PFIはモデルはそのままでデータを変更するだけで算出できます。

重要度（寄与度）の比較

それでは実際に、デフォルトの重要度、PFI、SHAPでそれぞれ重要度（寄与度）を算出していきましょう。

前提条件

本ソースコードは、Python3.7.5で起動するJupyter Lab上で実行されています。

また使用している各ライブラリのバージョンは以下の通りです。

  • numpy(1.20.3)
  • pandas(1.3.5)
  • scikit-learn (0.23.2)
  • matplotlib(3.5.1)
  • shap(0.40.0)

なお、今回はPyCaratは使用しません。

前回のPyCaratの記事で、タイタニックデータの場合は、ランダムフォレストが成績がよさそうだったので、ランダムフォレストのみで検証します。

タイタニックデータ取得＋α

今、さらっと「タイタニックデータの場合は」と書きましたが、今回もタイタニックのデータを使用します。

タイタニックのデータは以下のコードにより取得できます。

from sklearn.datasets import fetch_openml
X, y = fetch_openml(data_id=40945, as_frame=True, return_X_y=True)

 

今回、ちょっとした罠を仕掛けます。

以下のようなダミーの数値データを特徴量として追加します。

import numpy as np
seed = 42
rds = np.random.RandomState(seed=seed)
X["duummy_num"] = rds.randn(X.shape[0])

 

このようなデータを追加した理由は、後ほど説明します。

さらにデータを絞り込みます。

categorical_features = ["sex", "embarked"]
numerical_features = ["age", "sibsp", "parch", "fare", "pclass", "duummy_num"]
X = X[categorical_features + numerical_features]

ここで、カテゴリーデータと数値データの特徴量の名称の配列を作成しているのは、この後の処理に使用するためです。

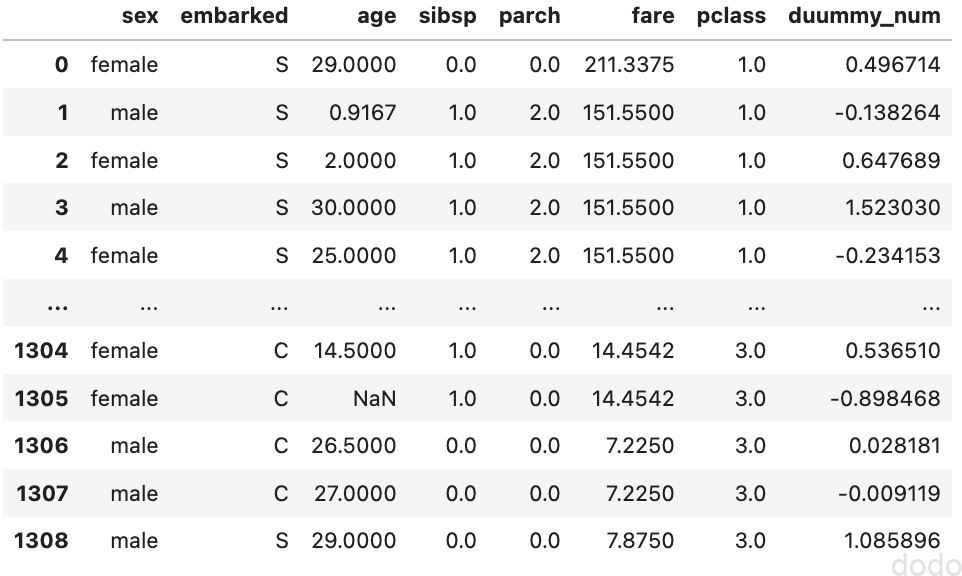タイタニックデータタイタニックデータ（ダミーデータ追加）

 

さらに教育データとテストデータに分類します。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)

パイプライン構築

scikit-learnの機能を用いてパイプラインを構築します。

まずは数値データについてのパイプラインを作成します。

from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler

numerical_transformer= Pipeline(
    steps=
    [
        ("imputer", SimpleImputer(strategy="mean")), 
        ("scaler", StandardScaler())
    ]
)

 

SimpleImputerによって欠損値を平均値で埋め、StandardScalerによってデータを規格化しています。

規格化は、今回のランダムフォレストのようなツリーベースの分類器ではあまり意味ないので、分類器をランダムフォレスト決め打ちならば、やらなくてもOKです。

次にカテゴリーデータのパイプラインを構築します。

from sklearn.preprocessing import OneHotEncoder
categorical_transformer = Pipeline(
    steps = 
    [
        ("imputer", SimpleImputer(strategy="most_frequent")),         
        ('onehot', OneHotEncoder(drop='if_binary'))
    ]
)

 

今回は、one-hot-encodingの手法を用いてカテゴリーデータを変換します。

OneHotEncoderは、微妙に使いにくいです・・
NaNデータがあるとエラーになる・・
→SImpleImputerで定数値で埋めるstrategy=”constant”を設定
→テストデータで未知のデータとなりエラーになる。
→handle_unknown=”ignore”を指定して無視させようとする→drop=”if_binary”と両立せずにエラーになる。
→SImpleImputerで定数値で埋めるstrategy=”most_frequent”に設定
（カテゴリーで最頻値ってどうよ・・）

となりました・・
OrdinalEncoder(カテゴリ値に順序を割り当てる方法）を使用する、もしくはパイプラインにこだわらないならばpandas.get_dummies()で変換するなどの方が良いかもしれません。

上記の２つのパイプラインを統合して変換器を作成します。

from sklearn.compose import ColumnTransformer
transformer = ColumnTransformer(
    [
        ("cat", categorical_transformer, categorical_features),
        ("num", numerical_transformer, numerical_features),
    ],
)

 

カテゴリーデータと数値データを分けるために、定義済みのカラム名の配列を使用しています。

最後にランダムフォレストの分類器と結合してパイプラインの完成です。

from sklearn.ensemble import RandomForestClassifier
pipe = Pipeline(
    [
        ("transformer", transformer),  
        ("classifier", RandomForestClassifier(n_estimators=50, random_state=42))
    ]
)

学習と検証

以下を実行してデータの変換とランダムフォレストによる学習をします。

pipe.fit(X_train, y_train)

 

学習データとテストデータで性能を検証すると以下のような結果になりました。

print(f"AUC(train): {pipe.score(X_train, y_train):.3f}")
print(f"AUC(test): {pipe.score(X_test, y_test):.3f}")
実行結果
AUC(train): 1.000
AUC(test): 0.808

まずまずの結果なので、このモデルを元に重要度を算出していきます。

他の記事で、交差検証しろとか、検証データとテストデータ分けろとか、散々書いてますが、今回は重要度を見たいだけなのでやっていません。ご了承ください。

重要度（デフォルト）

まずは、scikit-learnのRandomForestClassifierのデフォルトのロジックで重要度を算出します。

このデフォルトのロジックは、Mean Decrease Impurity(MDI)というもので、各特徴量によってツリーを分割した時の不純度（データのラベルの混ざり具合）の減少量（の木々の平均）を重要度の尺度としています。

乱暴な言い方をすれば、綺麗に分割できる特徴量ほど重要度が大きくなります。（仮にタイタニックデータで女性ならば必ず生存で男性ならば必ず死亡ならば、綺麗にツリーを分割できるので、重要となります。）

重要度はRandomForestClassifierの以下の属性で取得できます。

pipe['classifier'].feature_importances_
実行結果
array([0.21618001, 0.01821829, 0.00621902, 0.01140051, 0.18093579,
0.04626126, 0.03623733, 0.2044272 , 0.06636139, 0.21375921])

うん・・数値だけで何の特徴量だか分かりません・・

まずカラム名を取得する必要がありますが、パイプライン上でone-hot-encondingを実施しているので、OneHotEncoderのインスタンスにアクセスしてカラム名を取得する必要があります。

ohe = (pipe.named_steps['transformer'].named_transformers_['cat'].named_steps['onehot'])
categorical_features_oh = ohe.get_feature_names(input_features=categorical_features)
feature_names = np.r_[categorical_features_oh, numerical_features]

 

feature_namesの中身を表示すると以下のようになります。

array(['sex_male', 'embarked_C', 'embarked_Q', 'embarked_S', 'age', 
'sibsp', 'parch', 'fare', 'pclass', 'duummy_num'], dtype=object)

 

このカラム名の配列と重要度の値からpandasのSeriesを作成してデータをプロットします。

import pandas as pd
feature_importances = pd.Series(
    pipe[-1].feature_importances_, index=feature_names
).sort_values(ascending=True)

ax = feature_importances.plot.barh()
ax.set_title("Feature Importances")
ax.figure.tight_layout()
ax.figure.savefig('Feature-Importances-titanic.jpg', dpi=100)

 

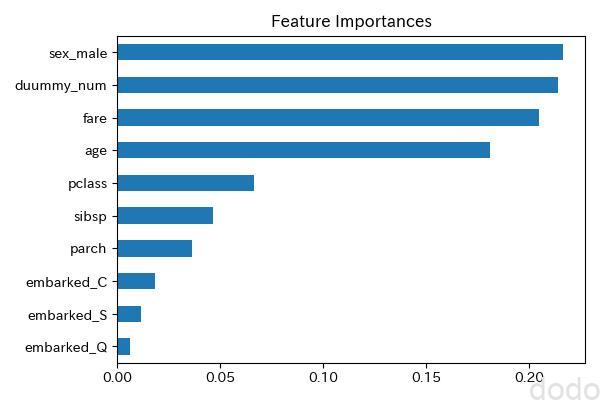重要度（デフォルト）重要度（デフォルト）

 

この時点で、おかしいのがわかると思いますが、ダミーの数値データが上位に来てしまっています。

ダミーの数値データはカーディナリティーが高い（取りうる値のバリエーションが多い）データとなっています。

このダミーの数値データを追加した事によって、ツリーの分割の不純度を基準とした重要度では、カーディナリティーが高いデータの重要度が大きくなってしまうという問題を再現しています。

このダミー以外は割とそれらしい特徴量（性別、年齢、運賃、クラス）が上位に来ていますが、こういう現象があると、この重要度を顧客に見せるのは不安が残ります。

Permutation Feature Importance(PFI)

ここでPFIの登場です。

概要については既に説明したので、早速、計算して可視化してみます。

from sklearn.inspection import permutation_importance

result = permutation_importance(
    pipe, X_test, y_test, n_repeats=10, random_state=seed
)

sorted_importances_idx = result.importances_mean.argsort()
importances = pd.DataFrame(
    result.importances[sorted_importances_idx].T,
    columns=X.columns[sorted_importances_idx],
)

ポイントとしては、以下となります。

  • 算出にデータが必要な事
    （つまり入力データが教師データかテストデータかで結果が異なる）
  • 複数回（上記では10回）実行して平均を取る事
    （データをシャッフルするためランダム性が生じるため）
  • 特徴量はパイプラインへの入力データの特徴量
    （つまりone-hot-encondeをしていない状態）

結果を可視化するには以下を実行します。（平均だけだと味気ないので、箱ひげ図で表示します。）

ax = importances.plot.box(vert=False, whis=10)
ax.set_title("Permutation Feature Importances (test data)")
ax.set_xlabel("Decrease in accuracy score")
ax.figure.tight_layout()
ax.figure.savefig('Permutation-Importances-titanic.jpg', dpi=100)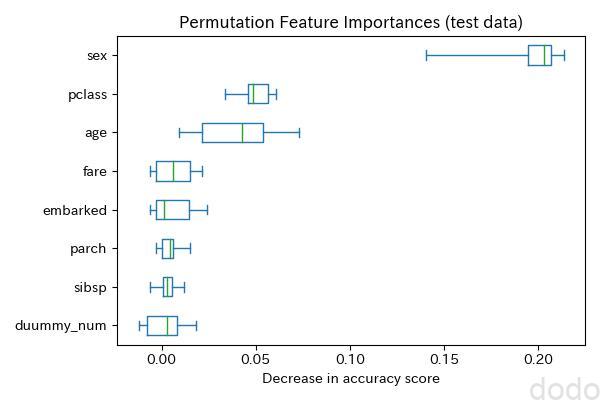
PFI重要度（PFI)

 

この方法だとダミーの数値データの重要度は低くなり、最もらしい特徴量が上位を占めていることがわかります。

SHAP

最後、SHAPでの寄与度も計算してみましょう。

import shap
shap.initjs()
explainer = shap.TreeExplainer(model=pipe['classifier'])
shap_values = explainer.shap_values(X=pipe['transformer'].transform(X_test))

 

前回の記事でPyCaratでラッピングしていた時は、わかりづらかったですが、以下のような手続きとなっています。

  1. 作成したモデルを引数にしてTreeExplainerのインスタンスを生成する。
  2. データを引数にしてSHAP値を計算する。（つまりデータによって値が異なる）

SHAP値はデータ毎の値なので、それらの絶対値を足し合わせて全体の寄与度を算出します。それを可視化したものが以下となります。

import matplotlib.pyplot as plt
shap.summary_plot(shap_values, feature_names=feature_names, class_names=["not survived","survived"],show=False)
plt.savefig('shap-summary.png', dpi=100)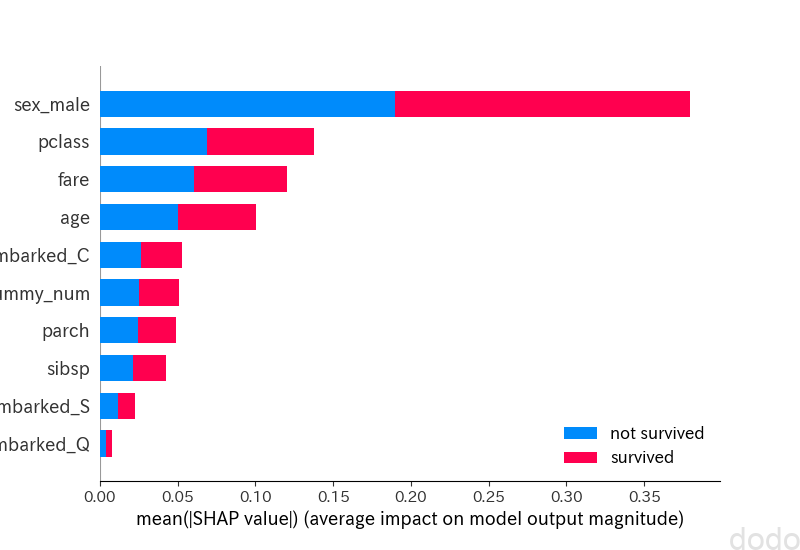
SHAP値SHAP値

SHAP値もダミーの数値データの寄与度は下位に来ているので、やはりそれなりに信頼できそうです。

まとめ

以上、重要度（寄与度）について、デフォルトの重要度、PFI、SHAP値を算出して比較してみました。

結論としては、デフォルトの重要度よりも、PFIもしくはSHAPを使用するべきです。

PFIとSHAPの使い分けは、それぞれ一長一短なので・・

計算コストを低く抑えるならばPFIを使う。
個別のデータへの寄与度を知りたければSHAPを使う。

といったように、状況によって使い分ければ良いかと思います。

こんな記事もおすすめ