データ分析の仕事をしていると、顧客から「とにかくディープラーニングを使ってほしい」と言われることがあります。
しかし、全てのデータの分析でディープラーニングが他のアルゴリズムに比べて優秀なわけではありません。
Kaggleなどのコンペでも、表データでは、LightGBMなどのツリーベースのアンサンブル・ブースティング手法の方がディープラーニングよりも良い結果が出ています。
なぜ、表データではディープラーニングはツリーベースのモデルに勝てないのか？
最近、その理由を考察した論文がarXivに投稿されて一部で話題になっていました。
https://arxiv.org/abs/2207.08815
本記事では、簡単なデータを使って、この論文に記載されている内容について検証していきます。
「検証していく」と言っても、たかだか１種類のデータで試すので、「試しにやってみた」程度のものです。
リンク先の論文では、さまざまな種類のデータ・アルゴリズムを用いて多角的に検証しているので、詳細について知りたい方は、リンク先の論文をご参照ください。
ツリーベースのモデルがディープラーニングに勝つ理由
ツリーベースのモデルがディープラーニングに勝つ理由について上記の論文では以下のような考察をしています。
ディープラーニングは平滑でないデータに適していない？
特徴量の微小な変化に対して出力結果が大きく変わるような「平滑でない」データでは、ディープラーニングよりもツリーベースのモデルの方が適しているとのことです。
出力結果を平滑化して学習した場合、ディープラーニングよりもツリーベースのモデルの方が精度に対する影響が大きい（より精度が悪くなる）という結果が出ています。
ディープラーニングは、元々、平滑でないデータへの適用が弱いので、ツリーベースのモデルほど平滑化した場合の影響が少ないということのようです。
このことから、平滑でない（分類で言えば、決定境界が複雑になるような）データについては、ツリーベースモデルに比べて性能が劣るのではないかと考察されています。
ディープラーニングは情報量が少ない特徴量に影響されやすいから？
表データでは特徴量の意味を考えた人為的な前処理が重要です。
データを可視化して相関関係を見たり、欠損値を埋めたり、違う特徴量同士を演算した特徴量を新たに追加することもあるでしょう。
しかし、どの特徴量が重要かは、やってみないとわからないので、あまり結果に影響しない特徴量が入力に混ざることは避けられません。
だとしても、そのような情報量の少ない特徴量は無視するように学習してくれるはず・・なのですが、ディープラーニングはそのような特徴量にも学習への影響を受けやすいとのことです。
このことから、重要でない特徴量が混ざっていた場合、ディープラーニングはツリーベースのモデルよりも性能が劣るのではないかと考察されています。
ディープラーニングは特徴量空間の回転に対して不変？
特徴量空間で特徴量を回転させたものを新たな特徴料として再定義したとします。
二次元で考えれば、以下の変換式によって特徴量\(X_1,X_2\)から特徴量\(X’_1,X’_2\)に変換して学習させるイメージです。
\begin{eqnarray}
\left( \begin{array}{cc} X’_1\\ X’_2\\ \end{array} \right)= \left(\begin{array}{cc} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \\ \end{array} \right) \left( \begin{array}{cc} X_1\\ X_2\\ \end{array} \right).
\end{eqnarray}
この変換を特徴量の多次元空間で実施すると、ツリーベースのモデルでは精度が著しく落ちますが、ディープラーニングでは精度が変わらないと記載されています。
しかし、この回転不変性こそが重要な特徴量と情報量が少ない特徴量との判別を困難にし、情報量が少ない特徴量を除外できなくなっていると考察されています。
タイタニックデータで試してみる。
紹介した論文では、様々なデータ・手法で試して考察しているので、たかだか１データで検証してもあまり意味はありませんが、お勉強も兼ねて実際に実装して、上記の理由について考えていきます。
前提条件
本ソースコードは、Python3.10.6で起動するJupyter Lab上で実行されています。
また使用している各ライブラリのバージョンは以下の通りです。
- numpy(1.22.4)
- pandas(1.4.3)
- scikit-learn (1.1.2)
Importと初期設定
必要なライブラリをインポートします。
import numpy as np
import pandas as pd
import scipy.stats as stats
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler,OneHotEncoder
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.compose import ColumnTransformer
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC,LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.covariance import MinCovDet
from catboost import CatBoostClassifier
import matplotlib.pylab as plt
import seaborn as sns
import copy
import warnings
import random
その他、warningの無視の設定、ランダムシード(seed)の指定などをします。
warnings.simplefilter('ignore')
sns.set()
seed = 42タイタニックデータ取得＋前処理
タイタニックデータを取得します。
X, y = fetch_openml(data_id=40945, as_frame=True, return_X_y=True)
特徴量の中から加工しないで使えそうな項目に絞ります。
CAT_FEATURES = ['sex', 'embarked']
NUM_FEATURES = ['age', 'sibsp', 'parch', 'fare', 'pclass']
X = X[CAT_FEATURES + NUM_FEATURES]
y = y.astype(int)
今回、情報量が少ない特徴量のテストのため、ダミーの特徴量を10個ほどランダム生成して追加します。
n_dummy_feature = 10
rnd = np.random
rnd.seed(seed=seed)
mean_uninform = rnd.normal(size = n_dummy_feature)
cov_uninform = rnd.normal(size = [n_dummy_feature,n_dummy_feature])
dummy_data = rnd.multivariate_normal(mean_uninform, cov_uninform, len(X))
DUMMY_FEATURES = [f'u{i}' for i in range(n_dummy_feature)]
df_dummy_data = pd.DataFrame(data=dummy_data, columns=DUMMY_FEATURES)
X_plus_dummy = pd.concat([X, df_dummy_data], axis=1)
ダミーの特徴量を含んだデータを、教師データとテストデータに分割します。
X_train, X_test, y_train, y_test = train_test_split(X_plus_dummy, y, stratify=y, random_state=seed)パイプライン構築
scikit-learnのパイプラインを構築します。
まずはパイプラインに組み込むための特徴両空間で特徴量を回転させるRotatorクラスを作成します。
class Rotator(BaseEstimator, TransformerMixin):
def __init__(self, seed=None):
if seed is not None:
self.seed = seed
self.rotate = True
else:
self.rotate = False
def fit(self, X, y=None):
return self
def transform(self, X):
if self.rotate:
rotation_matrix = stats.special_ortho_group.rvs(X.shape[1],random_state=self.seed)
return X @ rotation_matrix
else:
return X
引数で渡されたseedをもとにランダムに回転させた特徴量を返します。（指定しない場合は回転させません。）
Rotatorを組み込んだパイプラインを構築します。（今回は全体を関数化します。）
def pipeline(estimator,
cat_features=CAT_FEATURES,
num_features=NUM_FEATURES,
rotater=Rotator(),
**kwds):
numerical_transformer= Pipeline(
steps=
[
('imputer', SimpleImputer(strategy='mean')),
('scaler', StandardScaler())
]
)
categorical_transformer = Pipeline(
steps =
[
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(drop='if_binary'))
]
)
column_transformer = ColumnTransformer(
[
('cat', categorical_transformer, cat_features),
('num', numerical_transformer, num_features),
],
)
transformer = Pipeline(
steps =
[
('column', column_transformer),
('rotator', rotater)
]
)
model = Pipeline(
steps =
[
('transformer', copy.deepcopy(transformer)),
('classifier', copy.deepcopy(estimator))
]
)
model.set_params(**kwds)
return model
上記関数では、学習に使用する特徴量、Rotatorのインスタンスを渡せるようにしています。
分類器の指定
今回、比較のために以下の７つの分類器（アルゴリズム）を使用します。
- ロジスティック回帰
- 線形サポートベクターマシン
- サポートベクターマシン(RBFカーネル)
- 決定木
- ランダムフォレスト
- CatBoost
- MLP（隠れ層は１つ (784→100→10))
アンサンブル・ブースティングの実装にはXGBoost、LightGBMなどがありますが、今回はCatBoostを使用します。（今回のデータの場合、パラメータ未調整で最も性能が良かったので・・）
また、ディープラーニングとしては隠れ層が１つのMLPを使用します。（引用論文ではResNetを使用しています。）
estimators = {
#ロジスティック回帰(最適化にはliblinearを使用)
"LogisticRegression":LogisticRegression(C=3.63, random_state=seed),
#線形サポートベクターマシン
"LinearSVM":LinearSVC(C=3.63,random_state=seed),
#サポートベクターマシン(カーネルはRBF)
"SVM":SVC(gamma="auto", random_state=seed),
#決定木
"DecisionTree":DecisionTreeClassifier(random_state=seed, criterion='log_loss',
max_depth=3, min_samples_leaf=6,min_samples_split=4),
#ランダムフォレスト
"RandomForest":RandomForestClassifier(random_state=seed,max_depth=7,
min_samples_leaf=2, n_estimators=200),
#Catboost
"CatBoost":CatBoostClassifier(n_estimators=100, random_state=seed,logging_level='Silent'),
# ニューラルネットワーク（隠れ層は１つでユニット数は100 (784→100→10))
"MLP":MLPClassifier(max_iter=300, random_state=seed) ,
}
今回の趣旨としては、CatBoostとMLPだけあれば十分ですが、他の分類器がどのような挙動を示すのか興味があったの追加しました。（デフォルトパラメータで性能が良くなかった分類器は、事前にパラメータサーチを実施して最適なパラメータを設定しています。）
まずは回転、特徴量の増減、目的変数の平滑化などしない場合の各分類器のベースの性能を見てみましょう。
for k_est,estimator in estimators.items():
model_base = pipeline(estimator)
model_base.fit(X_train,y_train)
print(f'{k_est}:')
print(f' score(train) = {model_base.score(X_train,y_train):.3f}')
print(f' score(test) = {model_base.score(X_test,y_test):.3f}')出力結果
LogisticRegression:
score(train) = 0.782
score(test) = 0.802
LinearSVM:
score(train) = 0.784
score(test) = 0.811
SVM:
score(train) = 0.814
score(test) = 0.829
DecisionTree:
score(train) = 0.811
score(test) = 0.832
RandomForest:
score(train) = 0.858
score(test) = 0.838
CatBoost:
score(train) = 0.827
score(test) = 0.848
MLP:
score(train) = 0.833
score(test) = 0.835
この結果がベースとなります。
最後に可視化時に必要になる色リストを分類器の数だけ作成しておきます。
COLOR_LIST = ["r", "g", "b", "c", "m", "y", "k"]ディープラーニングは平滑でないデータに適していないのか？
論文に記載があった「ディープラーニングは平滑でないデータに適していない」かどうかをみていきます。
まずは、ガウシアンカーネルによって平滑化する関数を作成します。
def kernel_smoothing(X,y,length_scale):
if length_scale == 0:
return y
y_new = np.zeros(y.shape)
cov = length_scale * MinCovDet(support_fraction=None,assume_centered=False).fit(X).covariance_
for i in range(len(X)):
kernel = stats.multivariate_normal(mean=X[i], cov=cov, allow_singular=True)
pdf = kernel.pdf(X)
y_new[i] = np.dot(y, pdf) / np.sum(pdf)
return y_new
以下のコードによって特徴量が１つの場合の簡単なデータ（サインカーブ）で、この関数がどのような挙動を示すか確かめます。
X_kernel_test = np.arange(0,10,0.1)
y_kernel_test = np.sin(X_kernel_test)
plt.plot(X_kernel_test,y_kernel_test,label='base')
for i in (np.arange(0.1,1,0.2))**2:
plt.plot(X_kernel_test, kernel_smoothing(X_kernel_test.reshape(-1,1),y_kernel_test,i),label=f'scale:{i:.2f}')
plt.title('kernel smoothing test')
plt.legend()
plt.savefig(f"./kernel_test.png",bbox_inches='tight', pad_inches=0)
plt.show()
結果は以下のとおりです。
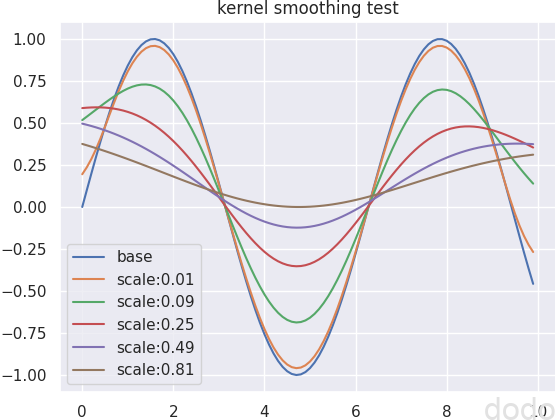平滑化のテスト
平滑化のスケールを大きくするほど、波のうねりが平滑化されていくことがわかります。
以下、各分類器で平滑化のスケールを変更して精度を比較するための関数を作成します。
def smoothing_compare(estimators, scales, X_train, y_train, X_test, y_test):
estimators_train_accs= []
estimators_test_accs= []
x_labels = []
for k_est,estimator in estimators.items():
#x軸ラベル設定
x_labels.append(k_est)
traiin_accs = []
test_accs = []
for scale in scales:
model = pipeline(estimator)
#モデルの前処理を利用してスムージング(スケーリングしない状態で実施)
X_train_for_smoothing = model['transformer'].fit_transform(X_train)
y_train_smooting = kernel_smoothing(X_train_for_smoothing, y_train, scale)
y_train_smooting = (y_train_smooting > 0.5).astype(int)
#モデル構築(教師データのラベルはスムージングしたものを使用)
model.fit(X_train,y_train_smooting)
traiin_accs.append(model.score(X_train,y_train))
test_accs.append(model.score(X_test,y_test) )
estimators_train_accs.append(traiin_accs)
estimators_test_accs.append(test_accs)
train_test_estimators_accs = [estimators_train_accs,estimators_test_accs]
fig, axs = plt.subplots(2, 1,figsize=(15, 20))
for i,estimators_accs in enumerate(train_test_estimators_accs):
ax = axs[i]
for x_label, accs, color in zip(x_labels, estimators_accs, COLOR_LIST):
ax.plot(scales, accs, 'o--', label=x_label, color=color)
ax.legend(loc='lower right')
title = 'train' if i==0 else 'test'
ax.set_title(f'{title} smoothing compare')
plt.savefig(f"./smoothing_compare.png",bbox_inches='tight', pad_inches=0)
plt.show()
コードに関しては詳しく説明しませんが、以下、ポイントのみ記載します。
- 平滑化された目的変数は、学習時のみ使用します。
（予測は元の目的変数で実施します。） - 分類なので平滑化した目的変数は0.5より大きい場合は１、0,5以下の場合は0とします。
この関数を使用して、スケール0(平滑化なし）から0.5刻みで4まで変化させて教師データ、テストデータそれぞれの精度を可視化します。
smoothing_compare(estimators, [0,0.5,1,1.5,2,2.5,3,3.5,4], X_train, y_train, X_test, y_test)
結果は以下のとおりです。
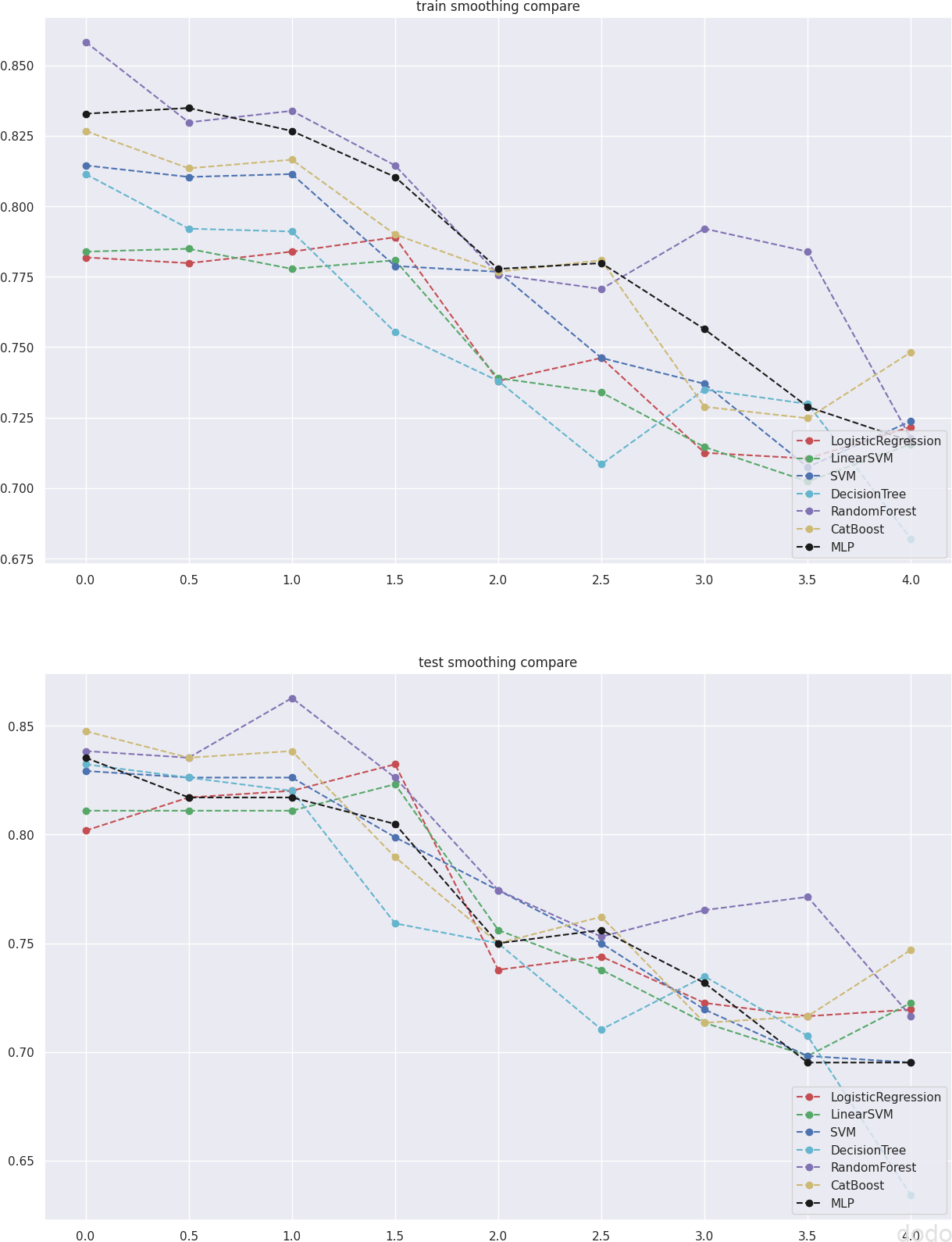平滑化（スケールを変更して比較）上図は教師データ、下図はテストデータの結果
総じて、どの分類器もスケールを大きくするにつれて精度が劣化しています。
MLPが特別、他の分類器に比べて精度の劣化が抑えられているか・・というとそうでもないですね・・
分類ではなく回帰データでやれば、違う結果が出るのかもしれませんが、少なくとも本記事のデータ・方法では、とりわけMLPが平滑化に強いような結果はみられませんでした。
ディープラーニングは情報量が少ない特徴量に影響されやすいのか？
次に「ディープラーニングが情報量が少ない特徴量に影響されやすいか」をみるために、特徴量の数を変えたときの挙動を見てみます。
特徴量を変更した場合の精度を可視化するために、以下の関数を作成します。
def feature_compare(estimators, features, X_train, y_train, X_test, y_test):
estimators_train_accs= []
estimators_test_accs= []
x_labels = []
for k_est,estimator in estimators.items():
#x軸ラベル設定
x_labels.append(k_est)
traiin_accs = []
test_accs = []
for _, feature in features.items():
model = pipeline(estimator,feature[0],feature[1])
model.fit(X_train,y_train)
traiin_accs.append(model.score(X_train,y_train))
test_accs.append(model.score(X_test,y_test) )
estimators_train_accs.append(traiin_accs)
estimators_test_accs.append(test_accs)
train_test_estimators_accs = [estimators_train_accs,estimators_test_accs]
fig, axs = plt.subplots(2, 1,figsize=(15, 20))
for i,estimators_accs in enumerate(train_test_estimators_accs):
ax = axs[i]
for x_label, accs, color in zip(x_labels, estimators_accs, COLOR_LIST):
ax.plot(features.keys(), accs, 'o--', label=x_label, color=color)
ax.axvline(x='BASE', color='r',ls='--')
ax.legend(loc='lower right')
title = 'train' if i==0 else 'test'
ax.set_title(f'{title} feature compare')
plt.savefig(f"./feature-compare.png",bbox_inches='tight', pad_inches=0)
plt.show()
特徴量を重要な２項目から、徐々に最初にフィルターした全特徴量まで増やします。（この状態をBASEとします。）
その後、さらにダミー特徴量を10個まで増やしていきます。
※重要度の順番は、以前のこちらの記事の結果に基づいています。
features = {'imp2': (['sex'], ['pclass']) ,
'imp3': (['sex'], ['pclass','fare']) ,
'imp4': (['sex'], ['pclass','age','fare']) ,
'imp5': (['sex','embarked'], ['pclass','age','fare']) ,
'imp6': (['sex','embarked'], ['pclass','age','fare','parch']) ,
'BASE': (CAT_FEATURES, NUM_FEATURES)}
for i in range(1,11):
features[f'+dum{i}'] = (CAT_FEATURES, NUM_FEATURES + DUMMY_FEATURES[:i])
feature_compare(estimators, features, X_train, y_train, X_test, y_test)
実行結果は以下のとおりです。
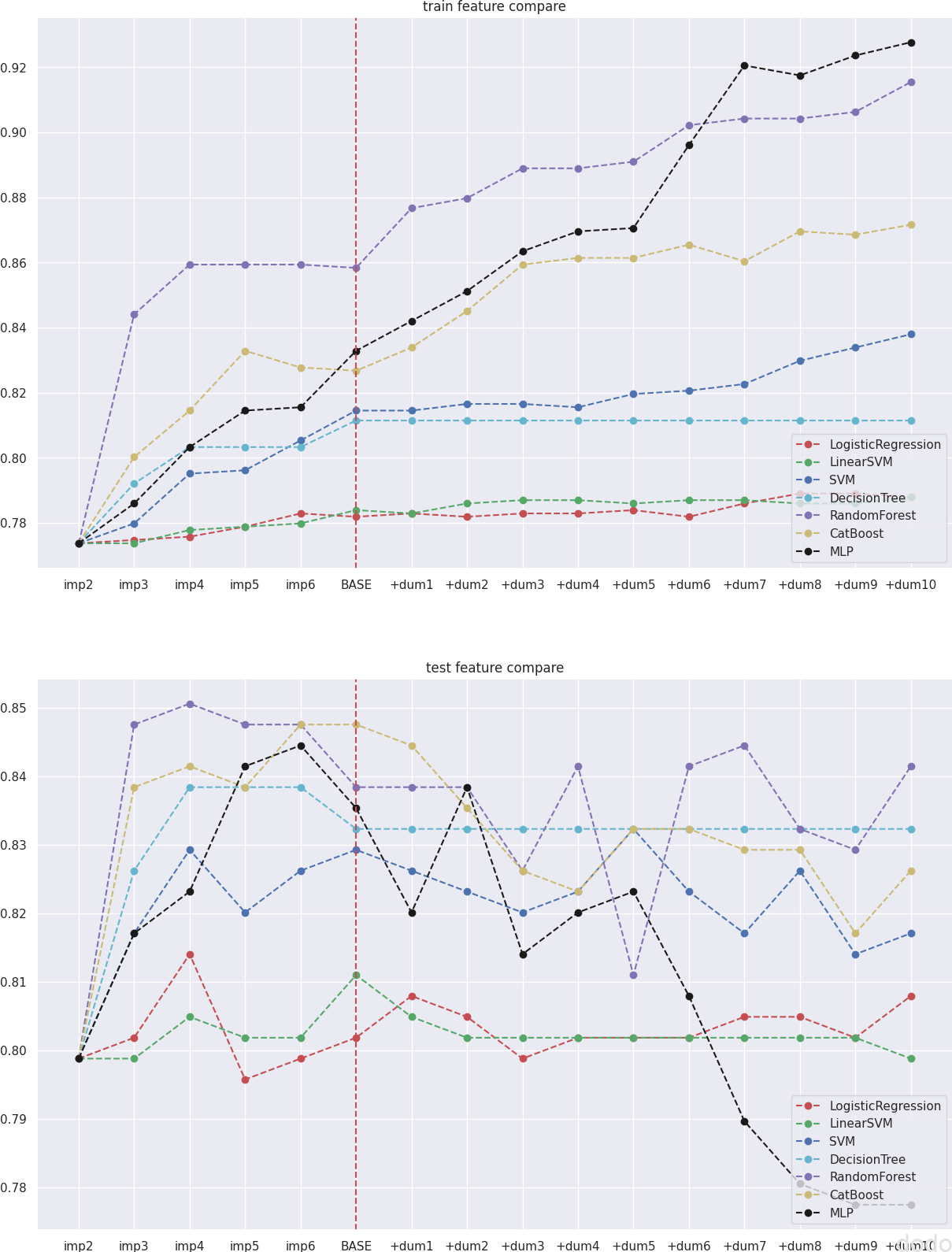特徴量を追加していき結果を比較 （上図は教師データ、下図はテストデータの結果）
特徴量の変化では明らかにMLP（黒点）が目立っています。
教師データで、ランダムなデータのダミー特徴量の追加でも精度が向上してしまっています。（他の分類器も上がってますが、MLPの上がり方は顕著です。）
そしてテストデータでは、ダミーの特徴量の追加につれて急激に精度が落ちています。（他の分類器はダミーの特徴量を追加していっても、それほど精度が下がっていません。）
これを見ると確かにディープラーニングは情報量が少ない特徴量に影響されやすいように見えます。
ロジスティック回帰、線形SVM、決定木はダミーの特徴量に対してほとんど影響を受けてないのも興味深いです。
ディープラーニングは特徴量空間の回転に対して結果が不変か？
最後に、「ディープラーニングは特徴量空間の回転に対して不変か」どうかを確かめます。
まずはパイプライン構築時に定義したRotatorがどのような動作をするのか簡単なデータを使用して確かめてみましょう。
以下は、二次元データ\(X_1,X_2\)=(1,2)を二次元平面で40回、ランダムに回転させるコードと、それを実行した結果です。
X_Rotate_test = np.array([[1,2]])
plt.plot(*X_Rotate_test.reshape(2,), '*', c='r')
base_random_state = np.random.RandomState(seed)
rndarr = base_random_state.randint(np.iinfo(np.int32).max, size=40)
for rnd in rndarr:
X_Rotate_test_rotate = Rotator(rnd).fit_transform(X_Rotate_test)
plt.plot(*X_Rotate_test_rotate.reshape(2,), '.')
plt.annotate(' (base)', xy=X_Rotate_test.reshape(2,) ,c='red')
plt.title('rotation test')
plt.savefig(f"./rotation_test.png",bbox_inches='tight', pad_inches=0)
plt.show()
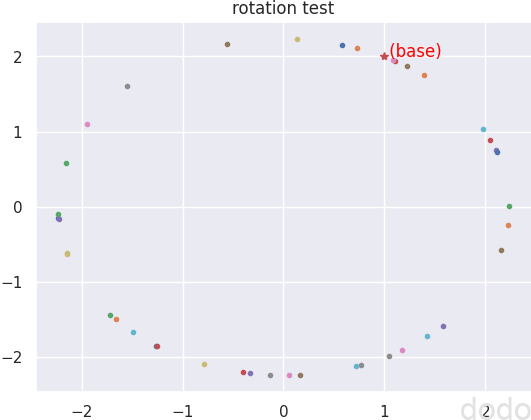回転データの生成
(base)と赤字で記載されている箇所に回転前の\(X_1,X_2\)=(1,2)のデータがあり、そのbaseデータを原点を中心に回転したデータがプロットされています。
以下のコードでは、特徴量数の次元で回転した新たな特徴量を生成して、そのデータで学習させます。
def rotate_compare(estimators, rndarr, X_train, y_train, X_test, y_test):
estimators_train_accs= []
estimators_test_accs= []
labels = []
train_test_base_accs = []
base_train_accs= []
base_test_accs= []
for k_est,estimator in estimators.items():
#ラベル設定
labels.append(k_est)
traiin_accs = []
test_accs = []
#回転していない場合
model = pipeline(estimator)
model.fit(X_train,y_train)
base_train_accs.append(model.score(X_train,y_train))
base_test_accs.append(model.score(X_test,y_test))
#回転させた場合
for rnd in rndarr:
#モデル構築
model = pipeline(estimator,rotater=Rotator(seed=rnd))
model.fit(X_train,y_train)
traiin_accs.append(model.score(X_train,y_train))
test_accs.append(model.score(X_test,y_test) )
estimators_train_accs.append(traiin_accs)
estimators_test_accs.append(test_accs)
train_test_estimators_accs = [estimators_train_accs, estimators_test_accs]
train_test_base_accs = [base_train_accs, base_test_accs]
fig, axs = plt.subplots(2, 1,figsize=(15, 20))
for i,(estimators_accs, base_accs) in enumerate(zip(train_test_estimators_accs,train_test_base_accs)):
ax = axs[i]
box_plt = ax.boxplot(estimators_accs,labels=labels,patch_artist=True)
for box, color in zip(box_plt['boxes'], COLOR_LIST):
box.set_facecolor(color)
ax.scatter(np.arange(1, len(base_accs)+1), base_accs, color='red', marker='*', s=100, zorder=2)
title = 'train' if i==0 else 'test'
ax.set_title(f'{title} rotate compare')
plt.savefig(f"./rotate_compare.png",bbox_inches='tight', pad_inches=0)
plt.show()
乱数を20個生成して、20回、ランダムに回転させた場合の精度を可視化します。
base_random_state = np.random.RandomState(seed)
rndarr = base_random_state.randint(np.iinfo(np.int32).max, size=20)
rotate_compare(estimators,rndarr,X_train,y_train,X_test,y_test)
結果は以下のようになります。
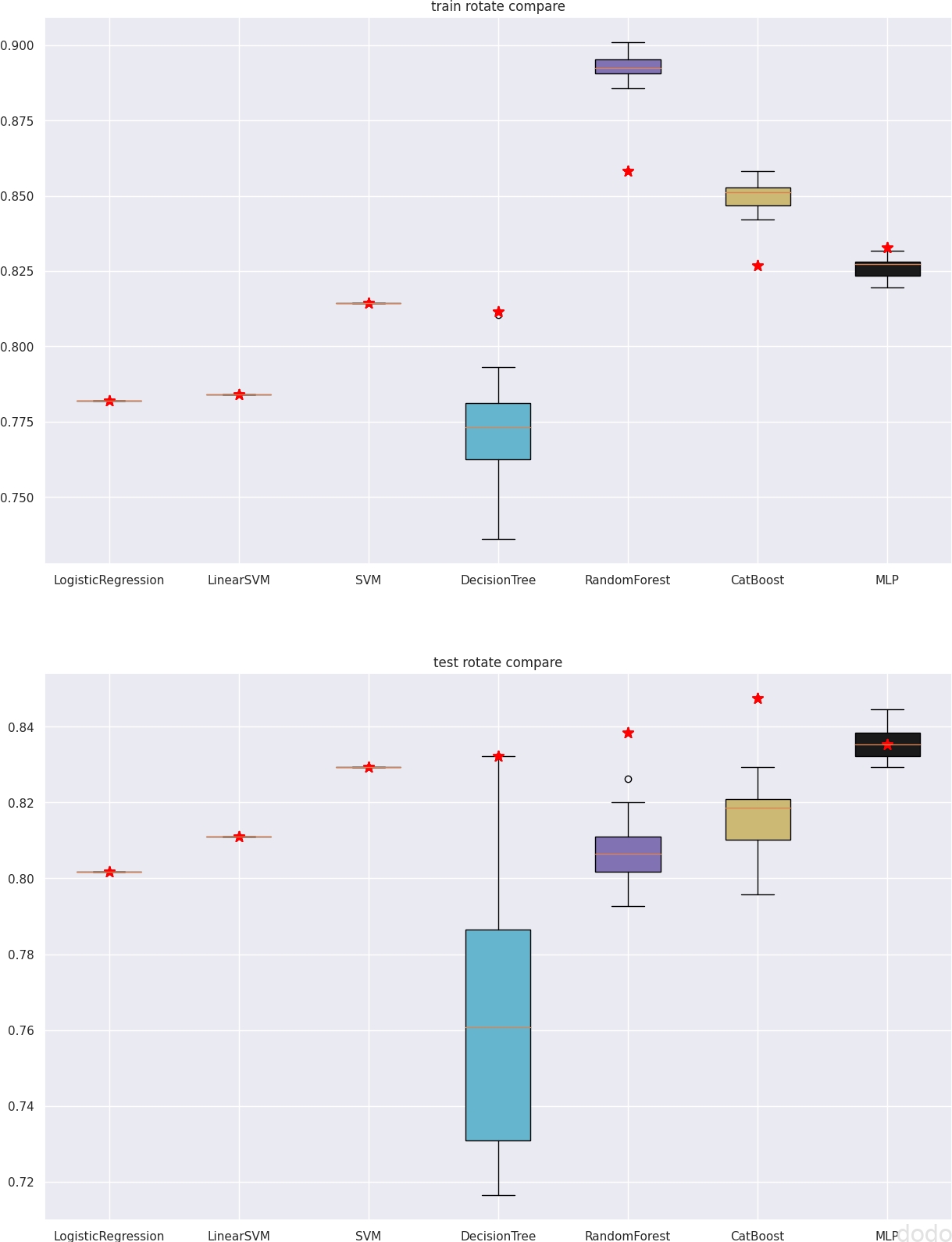特徴量空間で回転させて比較（上図は教師データ、下図はテストデータの結果）
赤い星印が回転していない元々のデータで学習した場合の精度で、箱髭図が回転した２０回のデータで学習した結果の分布を示したものです。
この結果からツリーベースの分類器（決定器、ランダムフォレスト、CatBoost）は回転させると精度が悪化していることがわかります。
それに対してMLPは回転に対して多少は結果が変わりますが、無回転の場合の精度を中心に分散しています。
ただし、ロジスティック回帰、SVMも回転に対して結果が不変なので、回転不変＝無意味な特徴量に影響されやすいというわけでもなさそうです。（ロジスティック回帰、SVMは無意味な特徴量の影響はそれほど受けていない。）
まとめ
以上、arXIvの論文をもとに「表データでディープラーニングがツリーベースモデルより弱い理由」について、実際に実装して確かめてみました。
論文では、以下３つの理由が挙げられていました。
- ディープラーニングは平滑でないデータに適していない。
- ディープラーニングは情報量が少ない特徴量に影響されやすい。
- ディープラーニングは特徴量空間の回転に対して結果が不変（❷の裏付け？）
本記事では❶については再現できず、❷❸については再現できました。
また❸の解釈については、ロジスティック回帰などの結果を見る限りは「回転不変＝情報量が少ないデータに影響されやすい」というわけでもなさそうです。
ただ、繰り返しますが、引用論文では様々なデータ、様々なパターンで検証しているのに対して、本記事では１データで「試しにやってみた」状態なので、この結果をもって何かしらを主張するものではありません。
データの種類によって、どのように結果が変化するのか・・興味がある方は本コードを利用・改変して、他の種類のデータなどで確かめてみてください。
