教師あり学習をやりたい。データは山ほどある。
しかしほとんどラベルがついていない・・
画像データなので一つ一つ画像を見ればラベルをつける事はできる・・
しかし面倒臭い・・・
そのような時のために半教師あり学習という手法があります。
半教師あり学習では、教師あり学習にプロセスに教師なし学習を組み込むことによって、少量のラベルありデータをもとにして、ラベルなしデータに対してラベルを付与することが可能です。
今回は、教師なし学習のKmeans法を利用して半教師あり学習を実装していきます。
事前準備
前提条件
本ソースコードは、Python3.10.6で起動するJupyter Lab上で実行されています。
また使用している各ライブラリのバージョンは以下の通りです。
- numpy(1.22.4)
- pandas(1.4.3)
- scikit-learn (1.1.2)
importと初期設定
まずは必要なライブラリをインポートします。
import os
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from sklearn.metrics import accuracy_score,plot_confusion_matrix
from sklearn.cluster import KMeans
import scipy.stats as stats
import matplotlib.pyplot as plt
import pickle
import warnings
import math
import copy
その他、warningの無視の設定、ランダムシード(seed)の指定、表の文字のデフォルトの大きの指定をします。
warnings.simplefilter('ignore')
plt.rcParams["font.size"] = 10
seed = 42
MNISTデータ取得
今回はMNISTデータを使用します。
MNISTデータは0から9までの数字の画像データです。
scikit-learnのfetch_openmlを使用してダウンロードします。
X, y = fetch_openml('mnist_784', return_X_y=True, as_frame=False)
28×28の画像データが70,000件取得できます。
最初の10件を可視化してみましょう。
fig, ax = plt.subplots(2, 5,figsize=(5, 3))
for i in range(0,10):
r = i // 5
c = i % 5
ax[r,c].set_xticks([])
ax[r,c].set_yticks([])
ax[r,c].set_title(y[i],fontsize=30)
ax[r,c].imshow(X[i].reshape(28, 28), cmap='Greys')
plt.savefig("./mnist_10.png")
plt.show()
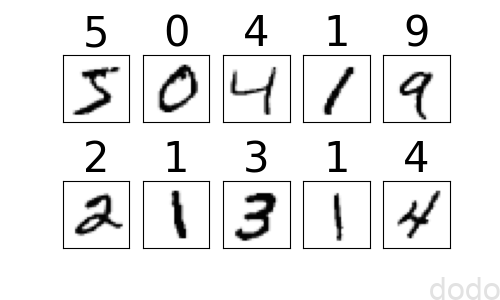 MNISTデータ
MNISTデータ
訓練データとテストデータを分離し規格化します。
X_train, X_test, y_train, y_test = train_test_split(
X, y, stratify=y, train_size=0.9, random_state=seed)
X_train = X_train /255
X_test = X_test /255
教師データの割合を90%として分割したので教師データのサイズは63,000件、テストデータのサイズは7,000件です。
共通関数作成
2つ共通関数を作成しておきます。
1つは、学習器をラッピングして、すでにモデルを保存済みの場合はそれをロードして返し、未保存の場合は新しく学習した学習器インスタンスを返す関数です。
今回、データの件数が多く、モデルの作成に時間がかかるので、学習した後は保存済みのモデルを使用するために作成しました。(ただしrebuild=Trueを指定すれば強制的にモデルを再構築します。)
def make_model(estimator, X, y, fileName, random_state, rebuild=False):
#モデル保存済みかつ再構築しない場合は読み込んで返す
if os.path.exists(fileName) and rebuild==False:
model = pickle.load(open(fileName, 'rb'))
else:
#モデル構築して保存
model = copy.deepcopy(estimator)
model.fit(X) if y is None else model.fit(X,y)
pickle.dump(model, open(fileName, 'wb'))
return model
もう一つは教師データとテストデータの予測結果をもとに混同行列を可視化する関数です。
最近の記事で精度だけ出してて味気なかったので、今回は混同行列くらいは可視化しようと思い作成しました。
def show_concusion_matrix(model, datas, title, label_names=None, col=3):
#グラフの行数
row = math.ceil(len(datas) / col)
#figureオブジェクト
fig = plt.figure(figsize=(10, 10))
for i,data in enumerate(datas):
#軸
ax = fig.add_subplot(row,col,i+1)
#confusion matrix
disp = plot_confusion_matrix(model, data[0], data[1], cmap=plt.cm.Blues,ax=ax,colorbar=False)
#精度(タイトル用)
y_predict = model.predict(data[0])
accuracy = accuracy_score(data[1],y_predict)
disp.ax_.set_title(f"{data[2]}: acc={accuracy:.3f}")
#軸ラベル
if label_names:
disp.ax_.set_xticklabels(label_names)
disp.ax_.set_yticklabels(label_names, rotation=90)
plt.savefig(f"./{title}-confusion_matrix.png",bbox_inches='tight', pad_inches=0)
plt.show()モデル作成
63,000件の教師データで学習
まずは普通に、て63,000件の教師データで学習したモデルで性能を評価します。
分類器には、ランダムフォレストを使用します。(以後の同様モデルでも同様)
いくつかのモデルのデフォルトパラメータで試してみたところランダムフォレストが最も良かったので選びました。
なお、最初はランダムサーチで交差検証をやって適切なパラメータを選択することもやろうとしていたのですが、精度がデフォルトパラメータに及ばないので止めました。(もっと真面目に時間をかけてやれば精度が向上するのかも知れませんが、今回目的はそれではないので・・)
model_normal = make_model(RandomForestClassifier(random_state=seed),
X_train, y_train, 'model_normal.pkl',
random_state=seed)
datas = [(X_train, y_train, 'train data'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_normal, datas, 'model_normal')
結果は以下の通りです。(左が教師データの混同行列、右がテストデータの混同行列です。)
 混同行列(63,000件の教師データで学習)
混同行列(63,000件の教師データで学習)
過学習はしていますが、テストデータでもまずまずの精度が出ています。
100件の教師データで学習
「教師データの数は63,000件あっても、そのうち100件しかラベルがついていない」
・・ということを想定して、教師データをラベルありデータの100件と、ラベルなしデータの62,900件に分割します。
X_train_small, X_train_remain, y_train_small, _ = train_test_split(
X_train, y_train, stratify=y_train, train_size=100, random_state=seed)
ラベルが付いている100件の教師データのみでモデルを構築して評価します。
model_small = make_model(RandomForestClassifier(random_state=seed),
X_train_small, y_train_small, 'model_small.pkl',
random_state=seed)
datas = [(X_train_small, y_train_small, 'train data(small)'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_small, datas, 'model_small')
結果は以下の通りです。
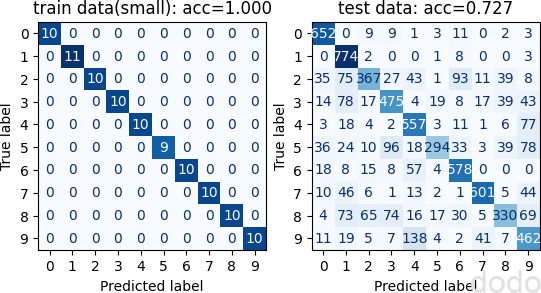 混同行列(100件の教師データで学習)
混同行列(100件の教師データで学習)
精度が0.967から0.727と約25%も下がってしまいました。
大半がラベルなしの状態で、ここから精度を上げるのはどうすれば良いでしょうか?
ラベルなしデータのラベルを予測して学習
ぱっと思いつくのは、以下の方法です。
- ラベルありデータ(100件)で作成したモデルでラベルなしデータ(62,900件)を予測
- ラベルなしデータに予測したラベルを付与する。
- 全63,000件の教師データで最終モデルを作成
図にすると以下のようなイメージになります。(データ数・列数は簡略化しています。)
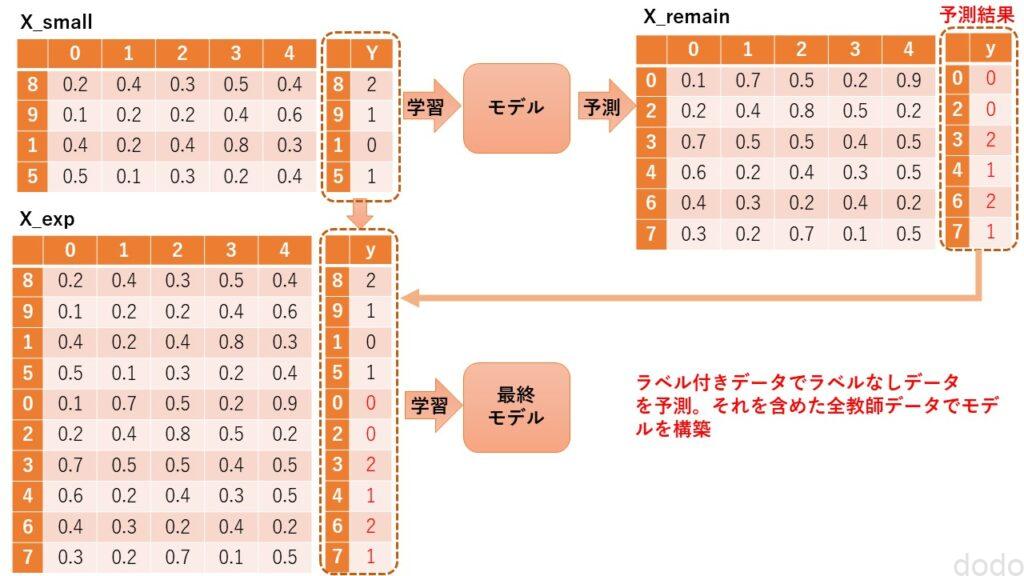 少数データモデルの結果からラベル付与→全教師デーアでモデル構築
少数データモデルの結果からラベル付与→全教師デーアでモデル構築
この方法を実装してみましょう。
上記の❶❷をコードにすると以下のようになります。
y_train_remain_predict = model_small.predict(X_train_remain)
X_train_exp = np.concatenate([X_train_small,X_train_remain])
y_train_exp = np.concatenate([y_train_small,y_train_remain_predict])
このデータを使用して、モデルを作成して評価します。
model_exp = make_model(RandomForestClassifier(random_state=seed),
X_train_exp, y_train_exp, 'model_exp.pkl',
random_state=seed)
datas = [(X_train_exp, y_train_exp, 'train data(exp)'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_exp, datas, 'model_exp')
結果は以下の通りです。
 混同行列(100件のデータで学習・予測したラベルを使用して学習(63,000件))
混同行列(100件のデータで学習・予測したラベルを使用して学習(63,000件))
100件の場合と比較して、精度は6%ほど向上しましたが、まだ十分なものとは言えません。
クラスタを代表する100件で学習
ここまでは、たまたまラベルが付いていた100件のデータで学習してモデルを作成していました。
次は、Kmeans法を利用することによってデータを特徴づけるような100件のデータを選別して、その100件を対象に手動でラベルを付与して学習させます。
教師なし学習では、データの特徴だけをみてクラスタリングをします。
具体的には以下のようにします。
- 63,000件のデータを100のクラスターにグルーピングする。
- 100のクラスターでそれぞれを代表するデータを選択する。(クラスターに重心に最も近いデータを代表するデータとする。)
- 選択した代表の100個のデータに手動でラベル付けをする。
- 代表の100件を学習させてモデルを作成する。
図にすると以下のようなイメージになります。(データ数・列数・クラスター数は簡略化しています。)
 Kmeans変換イメージ
Kmeans変換イメージ
 クラスターの代表データ(100件)でモデル作成
クラスターの代表データ(100件)でモデル作成
まずはKmeans法を利用して各クラスタを代表するデータを取得します。
model_kmeans = make_model(KMeans(n_clusters=100, random_state=seed),
X_train, None, 'model_kmeans.pkl', seed)
X_kmeans = model_kmeans.transform(X_train)
#代表する100件を取得
rep_idx = np.argmin(X_kmeans,axis=0)
X_train_rep = X_train[rep_idx]
取得した100件を可視化します。
fig, ax = plt.subplots(10, 10, figsize=(5, 5))
for i in range(0,100):
r = i // 10
c = i % 10
ax[r,c].set_xticks([])
ax[r,c].set_yticks([])
ax[r,c].imshow(X_train_rep[i].reshape(28, 28), cmap='Greys')
plt.savefig("./mnist_rep.png")
plt.show() 代表する100件
代表する100件
“これ↑”を見て頑張って手動でラベルを付けます。
y_train_rep = np.array(
[4,1,7,3,9,0,4,8,0,1,
9,6,5,5,2,2,8,3,2,9,
7,0,0,1,6,5,6,2,9,8,
6,0,7,7,2,1,1,0,3,2,
9,4,9,7,3,6,3,2,9,8,
2,6,5,6,6,4,8,3,5,7,
7,6,0,7,3,9,5,9,5,7,
4,5,3,2,1,1,8,0,0,5,
5,0,4,9,7,4,3,8,6,0,
4,5,6,0,8,2,7,2,6,1]).astype(str)
この代表データを使用して、モデルを作成して評価します。
model_rep = make_model(RandomForestClassifier(random_state=seed),
X_train_rep, y_train_rep, 'model_rep.pkl',
random_state=seed)
datas = [(X_train_rep, y_train_rep, 'train data(rep)'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_rep, datas, 'model_rep')
結果は以下の通りです。
 混同行列(クラスターを代表する100件で学習)
混同行列(クラスターを代表する100件で学習)
同じ100件にもかかわらずクラスタリングで特徴を捉えた100件のデータでは、適当な100件のデータで作成したモデルより9%も精度が向上しました。
代表データからラベルなしデータのラベルを予測して学習
100件のラベルありデータからラベルなしデータを予測した手法を、代表データの100件でも実施します。
図にすると以下のようなイメージになります。(データ数・列数は簡略化しています。)
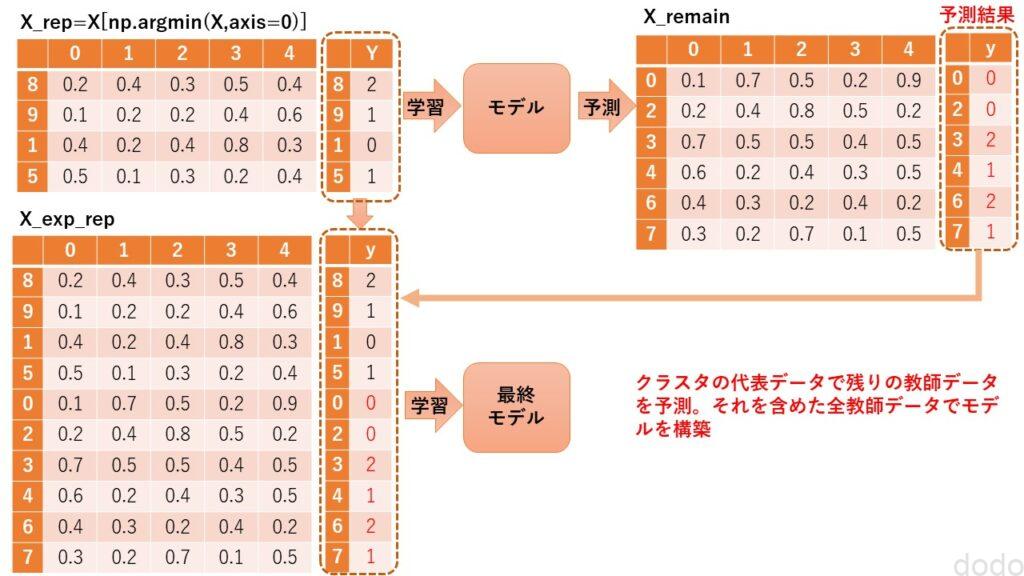 代表データモデルの結果からラベル付与→全教師デーアでモデル構築
代表データモデルの結果からラベル付与→全教師デーアでモデル構築
この方法でモデルを構築して評価します。
なお100件のラベルありデータで実施たい場合とほぼ同じコードとなります。(最初の予測モデルが異なるだけです。)
_train_remain_predict_rep = model_rep.predict(X_train_remain)
X_train_exp_rep = np.concatenate([X_train_small,X_train_remain])
y_train_exp_rep = np.concatenate([y_train_small,y_train_remain_predict_rep])
model_exp_rep = make_model(RandomForestClassifier(random_state=seed),
X_train_exp_rep, y_train_exp_rep, 'model_exp_rep.pkl',
random_state=seed)
datas = [(X_train_exp_rep, y_train_exp_rep, 'train data(exp_rep)'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_exp_rep, datas, 'model_exp_rep')
結果は以下の通りです。
 混同行列(代表100件のデータで学習・予測したラベルを使用して学習(63,000件))
混同行列(代表100件のデータで学習・予測したラベルを使用して学習(63,000件))
代表データ100件の場合と比較して7%ほど精度が向上しました。
ラベル伝搬した教師データで学習
代表データを元にしてラベルなしデータにラベルを付与する方法としてさらに良い方法があります。
同じクラスターに属するデータは同じラベルが付与されるとして、代表データと同じラベルをクラスタ内のデータに付与します。(これをラベル伝搬と言います。)
図にすると以下のようなイメージになります。(データ数・列数・クラスター数は簡略化しています。)
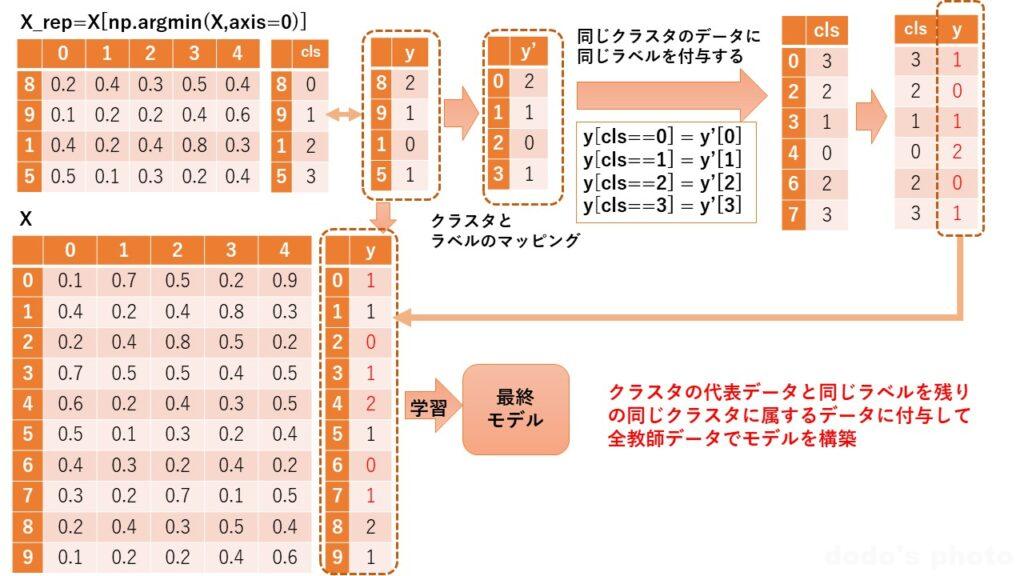 同じクラスターのデータに代表データと同じラベルを付与する。
同じクラスターのデータに代表データと同じラベルを付与する。
他のデータにラベル伝搬させる実装は以下のようになります。
y_train_prop = np.empty(len(y_train) ,dtype=np.str0)
for i in range(100):
y_train_prop[model_kmeans.labels_==i] = y_train_rep[i]
このデータ(63,000件)を使用して、モデルを作成して評価します。
model_prop = make_model(RandomForestClassifier(random_state=seed),
X_train, y_train_prop, 'model_prop.pkl',
random_state=seed)
datas = [(X_train, y_train_prop, 'train data(prop)'),(X_test, y_test, 'test data')]
show_concusion_matrix(model_prop, datas, 'model_prop')
結果は以下の通りです。
 混同行列(クラスターのラベルを伝搬させた63,000件で学習)
混同行列(クラスターのラベルを伝搬させた63,000件で学習)
代表のみ(100件)のモデルと比較して14%も向上しました。
「全て正しくラベル付けされた63,000件」のモデルと比較すると精度はまだ6%低いですが、完全にラベルなしの状態から、代表の100件のみ手動でラベル付けした後、他のデータへラベル伝搬しただけで、これだけの精度が出るのは、なかなか驚きです。
まとめ
以上、Kmeansを利用した半教師あり学習を実装して検証しました。
以下、結果を表にまとめます。
| 説明 | 教師データ件数 | テストデータ精度(%) | |
|---|---|---|---|
| 1 | 大量正解ラベル | 63,000 | 96.7 |
| 2 | 少数正解ラベル | 100 | 72.7 |
| 3 | 少数正解ラベル(100)+予測ラベル(62,900) | 63,000 | 77.6 |
| 4 | クラスター代表正解ラベル | 100 | 79.2 |
| 5 | クラスター代表正解ラベル(100)+予測ラベル(62,900) | 63,000 | 84.6 |
| 6 | クラスター代表正解ラベル(100)+伝搬ラベル(62,900) | 63,000 | 90.6 |
教師なし学習を組み合わせることによって、わずかなラベル付きデータのみで学習することができるのは、興味深いです。
なお、本記事は、以下の本の9章「教師なし学習のテクニック」を参考にしています。(ただし、コードも使用データも異なります。)
上記の本で使用しているデータでは、ラベル伝搬でオリジナルの教師データの精度に迫る精度が出ており、学習器やデータの種類によっては、かなり効果がある方法のようです。
また、「前処理として次元圧縮にKmeansを使用する」「ラベル伝搬で重心から遠い20%のデータを除外する」などの手法も紹介されており、興味のある方はご一読をお勧めします。