Coursera「機械学習」の1週目では、機械学習のモデルの最初の例として「単回帰」を説明し、実際にモデル（のパラメータ）を求める方法として「最急降下法」について説明しています。
単回帰分析は教師あり学習の「回帰」のもっとも初歩的な手法で、目的変数(\(y\))を１つの変数(\(x\))から予測するモデルです。
単回帰
講座では「家の広さ」から「家の販売価格」を予想する問題を例にとって説明しています。
以下のようなm個の「家の広さ」と「家の販売価格」の既知のデータ（正解がわかっている、つまり実際にその金額で売れたもの）があるとします。
| 家の広さ(feet\(^2\)) (\(x\)) | 家の販売価格(単位1000$) (\(y\)) |
|---|---|
| 2104 (\(x^{(1)}\)) | 460 (\(y^{(1)}\)) |
| 1416 (\(x^{(2)}\)) | 232 (\(y^{(2)}\)) |
| 1534 (\(x^{(3)}\)) | 315 (\(y^{(3)}\)) |
| 852 (\(x^{(4)}\)) | 178 (\(y^{(4)}\)) |
| ・・・ | ・・・ |
| ・・・ | ・・・ |
| 233 (\(x^{(m)}\)) | 121 (\(y^{(m)}\)) |
これらを「教師データ」として学習させる事によって、「家の広さ」と「家の販売価格」の関係性を見出して、これから売ろうとしている家の広さから販売価格を予測しようとするものです。
「単回帰」では、販売価格は、家の広さ\(x\)から以下の式で予測できるものとします。
$$h_\theta(x)=\theta_0+\theta_1x$$
この\(h_\theta(x)\)が販売価格を予測するためのモデルです。（hypothesisで直訳すると「仮説」ですが、本記事では「モデル」と記載します。）
数学的には\(x\)の関数で、この式を満たすような\(\theta_0\)と\(\theta_1\)が求められれば、これから売ろうとしている家の販売価格を予想できるようになります。
この事をグラフでイメージすると、教師データの「家の広さ」と「販売価格」をプロットしたデータのグラフを「まあまあ」満たすような直線を引く事になります。
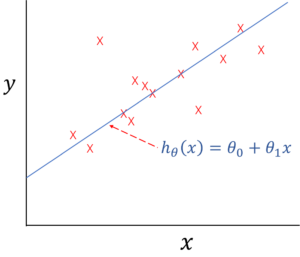単回帰モデルイメージ目的関数
上記で「まあまあ」と言ったように、世の中複雑なので、全ての教師データを完璧に満たすような\(\theta_0\)と\(\theta_1\)は求められません。
なので、モデルから計算された\(h_\theta(x^{(i)})\)と実際の値である\(y^{(i)}\)がなるべく近い値になるような\(\theta_0\)と\(\theta_1\)を求める事になります。
具体的には、目的関数\(J(\theta)\)を以下のように定義して、この目的関数を最小にするような\(\theta_0\)と\(\theta_1\)を求めます。
$$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$
因みに、この目的関数について「なんで二乗するの？」というよくある質問があります。
そして、「ただの引き算だったらプラスマイナスが相殺されちゃうからだよ」「いやいやだったら絶対値でいいじゃん。二乗する必要ないじゃん・・」といったやり取りをよく見かけます。
フォーラムでも同様な質問があって、それに対するメンターの回答は「絶対値だと微分不可能（傾きが求められない）な点があり計算上、都合が悪い。」との事でした。
確かに\(x\)の値が０の場合は微分不可なので都合悪いですね。
ただ、色々調べると他の理由として「\(h_\theta(x^{(i)})\)と\(y^{(i)}\)の差を誤差として、それが正規分布に従うとした場合に最尤法で求める場合と同じ結果になる」からというものがあり、個人的にはその説明が一番しっくりきました。（脱線するので詳しくは説明しませんが・・）
最急降下法
では目的関数\(J(\theta)\)を最小にするための\(\theta_0\)と\(\theta_1\)はどうやって求めればよいのでしょうか。
ここでは最急降下法という手法を使います。
高校数学を覚えている方ならば、\(J(\theta)\)を\(\theta_0\)と\(\theta_1\)で微分すれば、それぞれの軸での傾きが得られることがわかると思います。
なので、\(J(\theta)\)を最小にするためには、ある点での傾きを見て、その値が正（\(J(\theta)\)が大きくなる方向）ならば、\(\theta\)を小さくして、その値が負（\(J(\theta)\)が小さくなる方向）ならば、\(\theta\)を大きくしていき、傾きがだいたい０になった時点での\(\theta_0\)と\(\theta_1\)を求めれば良い事になります。
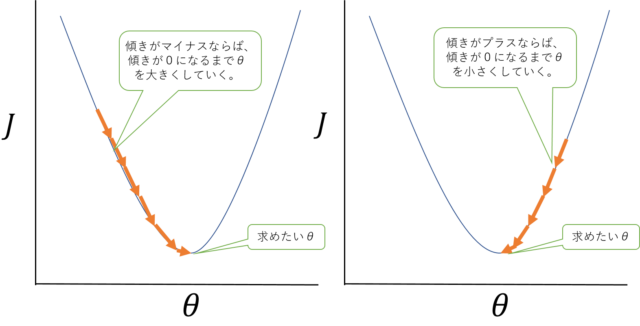最急降下法イメージ(\(\theta_0\)は固定して\(\theta_1\)だけに簡略化して\(\theta\)としている。)これを式で表すと以下のようになります。
\begin{align}
\theta_j&:=\theta_j-\alpha \frac{\partial}{\partial \theta_j} J(\theta_0,\theta_1) \;\;\;(\text{for } j=0,1 )
\end{align}
※「\(:=\)」は代入するという意味です。
まずは\(\theta_0\)と\(\theta_1\)を適当に選んで、\(\theta_0\)と\(\theta_1\)が収束するまで上記の式を繰り返し実行する事になります。
そして単回帰の場合だと(2)で定義した目的関数\(J(\theta)\)を微分して具体的に以下のような数式で表す事ができます。
\begin{align}
&\theta_0:=\theta_0-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)}) \\
&\theta_1:=\theta_1-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)} \\
\end{align}
ここで\(\alpha\)は一回の実行でどれだけ\(\theta_0\)と\(\theta_1\)を変化させるかを調整するためのパラメータになります。（学習率といいます。）
\(\alpha\)が大きすぎると、最小点を飛び越えてしまっていつまで経っても落ち着かずに発散してしまう場合があり、かと言って小さくしすると収束するまでの回数が多すぎて時間がかかってしまいます。
よって試行錯誤で\(\alpha\)の値は「いい具合」に選ぶ事になります。
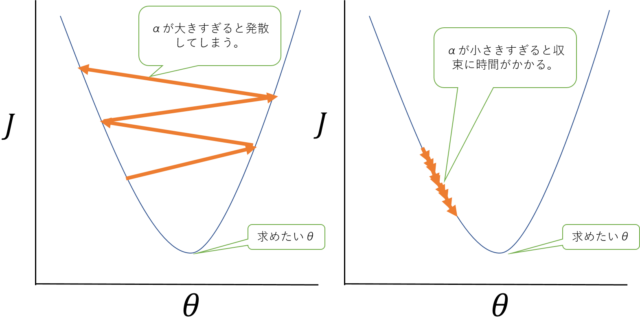最急降下法（αの調整について）なお最急降下法は、単回帰だけのものではなく、他の機械学習のモデルでも使用することができます。
ただし、単回帰と異なって、目的関数の最小点が１つとは限らないので、初期値の選び方によっては、局所的な最小点に落ち着いて、最も最小となる点に収束しない場合があるの注意が必要です。
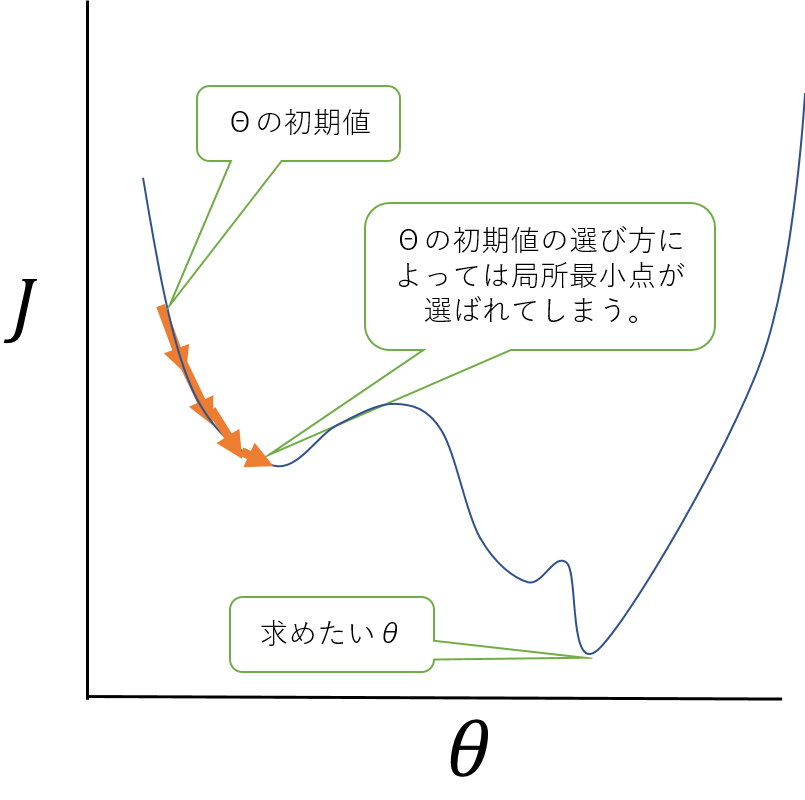最急降下法（局所最小）なお、最急降下法とか使わなくても、普通にこれ解析的に\(\theta_0\)と\(\theta_1\)を求められるんじゃないの？と思った方・・はい、数学的には正しいです。
数学的には正しいのですが、現実的には色々使えない場合があって・・・それについては、第２週目で言及しており受講記の記事でも書く予定です。
実際にやってみた。
第1週目はコーディングする課題はないのですが、第2週目の課題のOctaveのプログラムをちょっとだけ拝借して、実際の最急降下法がどのようなイメージで実行されるかを確かめてみました。
以下のような５つほどのデータを元に最急降下法により単回帰モデルを構築します。
| (\(x\)) | (\(y\)) |
|---|---|
| 1 | 4.2 |
| 2 | 7.1 |
| 3 | 7.3 |
| 4 | 8.3 |
| 5 | 8.2 |
\(\theta_0\)と\(\theta_1\)の初期値は0、αは0.1として上記の(4)(5)により最急降下法を実行します。
(4)(5)を１回だけ実行した場合は\(h_\theta(x)\)は以下の左図の直線になり、目的関数\(J(\theta)\)は以下の右図のように\(\theta_0\)と\(\theta_1\)の等高線で表した時にプロットされている点となりまます。
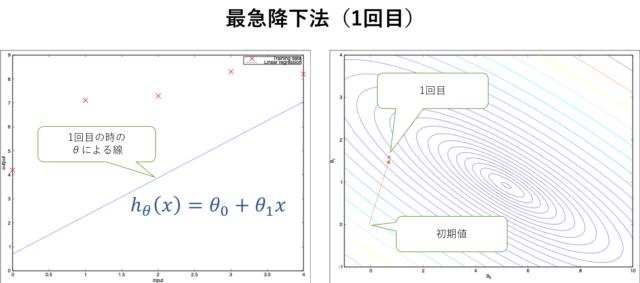最急降下法(１回目)30回実行すると以下のようになります。(まだ収束していません。）
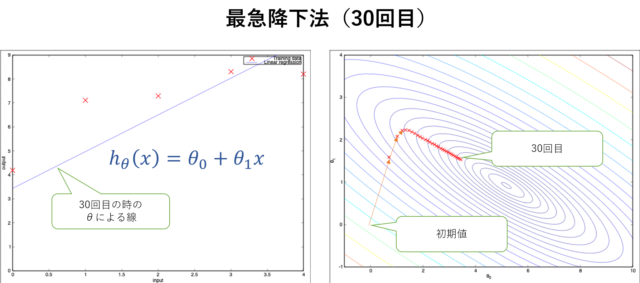最急降下法(30回目)このケースでは314回目で収束して、最適な\(h_\theta(x)\)が求められました。
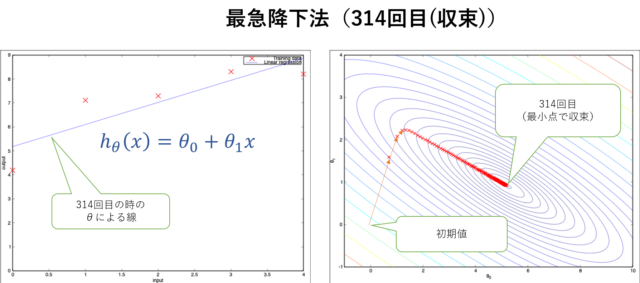最急降下法(314回目)右図から\(J(\theta)\)が一番最小となるように\(\theta_0\)と\(\theta_1\)が決定されるのがわかると思います。
まとめ
1週目の後半は、単回帰分析についての講義でした。
機械学習に幻想を抱いている方は、「これのどこが機械学習（AI）なの？単なる数学じゃん」と思うかもしれません。
ただ、これがディープラーニングになったとしても、モデルを表現する関数\(h_\theta(x)\)が複雑になったり、目的関数\(J(\theta)\)を求める方法が複雑になったりするだけで本質的にはやることは変わりません。
次回は、２週目の重回帰分析についてまとめていこうと思います。
