いわゆる「AI」を期待しているお客様に対して、ロジスティック回帰を使いますとか言おうものならば「それのどこがAIだ！」と言われる可能性があります。
しかしロジスティック回帰は、機械学習における分類問題の基本的なアルゴリズムであり、しかもビッグデータとかでないならば、それなりの精度がでます。（この記事参照）
そしてロジスティック回帰は、ベースは実に単純なロジックなので、スクラッチで実装するのも（最適化での様々な工夫をしなければ・・）それほど難しくはありません。
本記事では、ロジスティック回帰をスクラッチで実装する方法について記載します。
ロジスティック回帰とは？
ロジスティック回帰についてちょっとだけ簡単に説明します。（ちょっとだけです。）
詳細については、以下の記事をご参照ください。
ロジスティック回帰における最急降下法による最適化は以下のような流れになります。
- データの特徴量から分類するクラスに線形変換をする。(パラメータ(\(W,b\)))
- ❶の結果をソフトマックス関数で変換する。(\(\tilde{y}\))
- 変換結果(\(\tilde{y}\))と正解データ(\(y\))の差が小さいほど値が小さくなる損失関数を定義してその値を求める。
- 損失関数の\(W,b\)での微分値を求めて、損失関数を小さくするようにするような新しい\(W,b\)を求める。
❶から❹までを\(W,b\)が収束するまで繰り返します。
図にすると以下のようなイメージになります。
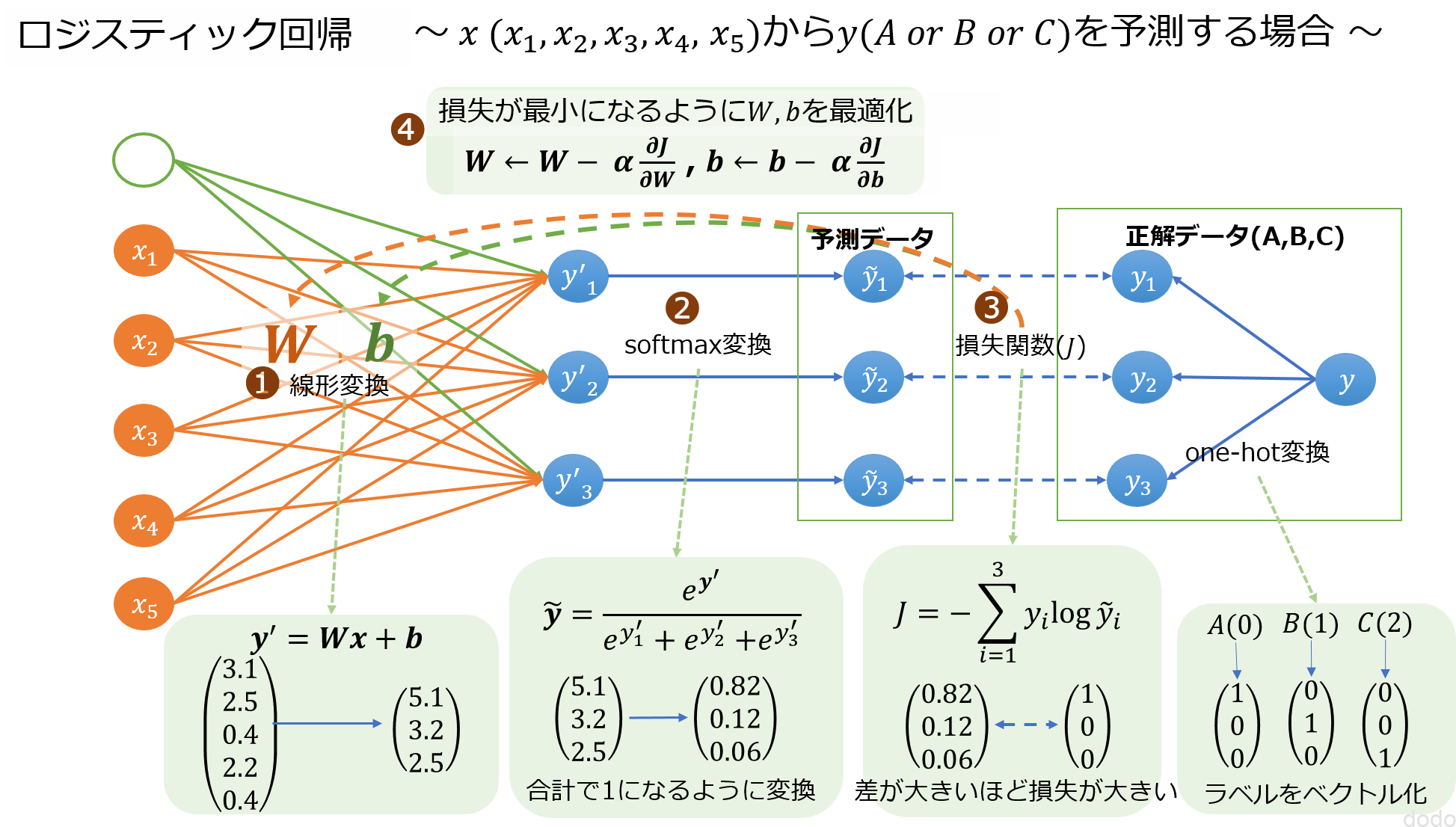ロジスティック回帰イメージ（最急降下法の場合）ロジスティック回帰の実装
それでは、上記の流れを基にして実装していきましょう。
ライブラリのインポート
まずは行列の数値計算に必要なnumpyとグラフ作成のためのmatplotlibをインポートします。
import numpy as np
%matplotlib inline
import matplotlib.pyplot as pltパラメータの初期化
線形変換に必要なパラメータ\(W,b\)の初期化（全要素を１）を実装します。
def init_parameter(n_classes, n_futures):
W = np.ones((n_futures, n_classes))
b = np.ones((1, n_classes))
return W,bロジスティック回帰ならば、全ての要素を１に初期化しても問題ないですが、ニューラルネットワークの場合は全て１だと各ユニットのパラメータが同じ値に収束してしまうので、ランダムな値に設定する必要があります。
\(W\)は[特徴量の数]×[分類クラス数]の行列、\(b\)は１×[分類クラス数]の行列となります。
線形変換
線形変換を実装します。（前節❶に該当)
def linear_trans(X,W,b):
return np.dot(X,W) + b
\(X\)は[サンプル数]×[特徴量数]の行列、戻り値は[サンプル数]×[分類クラス数]の行列となります。
数式で表すと以下のような式になります。
$$ y = X\cdot W + b $$
ソフトマックス関数
ソフトマックス関数を実装します。（前節❷に該当)
def softmax(Z):
return np.exp(Z) / np.sum(np.exp(Z),axis=1)[:,np.newaxis]
数式で表すと以下のような式になります。
$$ y = \dfrac{e^{z}}{ \sum_{i=1}^{m} e^{z_{i}}} $$
損失関数
損失関数をを実装します。（前節❸に該当)
def get_loss(Y_true,Y_pred):
return -np.sum(Y_true * np.log(Y_pred)) / Y_true.shape[0]
数式で表すと以下のような式になります。
$$J(W,b)= -\frac{1}{m} \sum_{i=1}^{m} y_{i} \log(\tilde{y}_{i})$$
パラメータの最適化
損失関数の\(W,b\)での微分値から新しい\(W,b\)を求めるロジックを実装します。（前節4 ❹に該当)
def get_optimized_parameter(X, Y_true, Y_pred, W, b, alpha):
W -= alpha * np.dot(X.T, Y_pred - Y_true) / X.shape[0]
b -= alpha * np.dot(np.ones((1, X.shape[0])), Y_pred - Y_true) / X.shape[0]
return W, b
数式で表すと以下のような式になります。
\begin{eqnarray}W&:=&W-\alpha \frac{1}{m}X^{T}(\tilde{y}-y)\\b&:=&b-\alpha \frac{1}{m}(\overbrace{1,\cdots,1}^{m})(\tilde{y}-y)\end{eqnarray}
ここで\(\alpha\)は学習率と呼ばれるものです。
\(\alpha\)が大きすぎると収束しないで発散したり、小さすぎると収束が遅かったりするので、うまく収束するように調整します。
最適化の全体の処理
最後に最適化の全体の処理(❶〜❹を繰り返す処理)を実装します。
まずは性能の測定のために精度を算出する関数を実装します。
def get_predict(Y_pred_proba):
Y_arg_max = Y_pred_proba.argmax(axis=1)
Y_pred = np.zeros(Y_pred_proba.shape)
for i in range(Y_pred_proba.shape[0]):
Y_pred[i, Y_arg_max[i]] = 1
return Y_pred
def get_accuracy(Y, Y_pred_proba):
Y_pred = get_predict(Y_pred_proba)
count = 0
for i in range(len(Y)):
if (Y[i]==Y_pred[i]).all():
count += 1
return count / len(Y)
１番目の関数「get_predict」は確率として出力された予測値を1,0に変換します。（最も値が大きい要素を１として、それ以外を０とする。）
2番目の「get_accuracy」は、正解データと「get_predict」の予測結果から精度を算出します。
さらに繰り返しの過程で損失関数の値（ロス）と精度をグラフ化したいため以下のような関数を実装します。
def plot_iteration(train_loss_list,train_acc_list,valid_loss_list,valid_acc_list):
fig = plt.figure(figsize=(15, 5))
ax1 = fig.add_subplot(1,2,1)
ax1.set_xlabel("iterartion",fontsize=20)
ax1.set_ylabel("loss",fontsize=20)
ax1.plot(train_loss_list,label="train")
ax1.plot(valid_loss_list,label="valid")
ax1.legend(fontsize=20)
ax2 = fig.add_subplot(1,2,2)
ax2.set_xlabel("iterartion",fontsize=20)
ax2.set_ylabel("accuracy",fontsize=20)
ax2.plot(train_acc_list,label="train")
ax2.plot(valid_acc_list,label="valid")
ax2.legend(fontsize=20)
plt.savefig("./loss-acc-iteration.png")
plt.show()
最後にここまで作成した関数を使用して全体の処理を実行する関数を実装します。
def optimize(X_train, Y_train, X_valid, Y_valid, alpha, iter_max):
#教師データのロス
train_loss_list = []
#教師データの精度
train_acc_list = []
#テストデータのロス
valid_loss_list = []
#テストデータの精度
valid_acc_list = []
#W,bの初期化
W,b = init_parameter(Y_train.shape[1],X_train.shape[1])
#予測結果の初期値
Y_train_pred = softmax(linear_trans(X_train,W,b))
for count in range(iter_max):
#教師データで最適化
W, b = get_optimized_parameter(X_train, Y_train, Y_train_pred, W, b, alpha)
#教師データと検証データを最適化したW,bで予測
Y_train_pred = softmax(linear_trans(X_train,W,b))
Y_valid_pred = softmax(linear_trans(X_valid,W,b))
#教師データと検証データのロスを保存
train_loss_list.append(get_loss(Y_train,Y_train_pred))
valid_loss_list.append(get_loss(Y_valid,Y_valid_pred))
#教師データと検証データの精度を保存
train_acc_list.append(get_accuracy(Y_train, Y_train_pred))
valid_acc_list.append(get_accuracy(Y_valid, Y_valid_pred))
plot_iteration(train_loss_list,train_acc_list,valid_loss_list,valid_acc_list)
return W,b実装したロジックの検証
MNIST
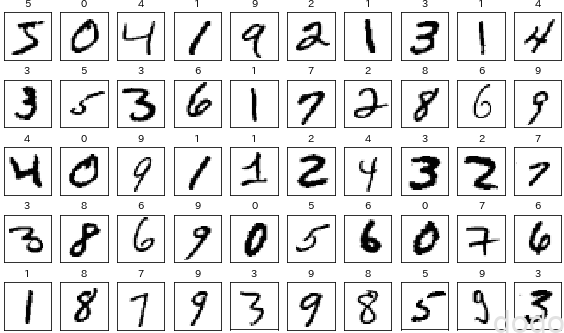
スクラッチで実装したロジスティック回帰をMNISTで検証します。
MNISTは手書き文字の画像データ(28×28)となっており、以下のコードでダウンロードできます。
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1,)
データの一部を可視化すると以下のようになります。
fig, ax = plt.subplots(5, 10,figsize=(10, 6))
for i in range(0,50):
x = i % 10
y = i // 10
ax[y,x].set_xticks([])
ax[y,x].set_yticks([])
ax[y,x].set_title(mnist.target[i],fontsize=10)
ax[y,x].imshow(mnist.data[i].reshape(28, 28), cmap='Greys')
plt.savefig("./mnist_evaluate-ec.png",bbox_inches='tight', pad_inches=0)
plt.show()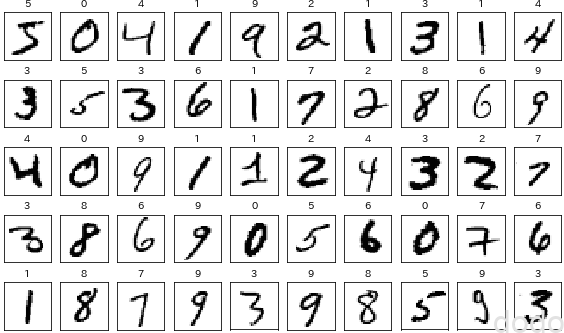
MINSTの画像を可視化したものデータの分割
データは全部で70,000件ありますが、今回は、その一部のみを教師データ、検証データ、テストデータとして利用します。
sckit-learnには良きにデータを分割してくれる関数(sklearn.model_selection.train_test_split)がありますが、今回はスクラッチついでに、スクラッチでデータを分割・抽出する関数も作成します。
def get_split_data(X, y, size_ratio):
#データ数
n_samples = X.shape[0]
#分類クラス数
n_classes = len(set(list(y)))
#教師データ最大index
n_train_max = round(n_samples * size_ratio[0])
#検証データ最大index
n_valid_max = n_train_max + round(n_samples * size_ratio[1])
#テストデータ最大index
n_test_max = n_valid_max + round(n_samples * size_ratio[2])
#シャッフル
np.random.seed(0)
p = np.random.permutation(n_samples)
X_shuffle = X[p,:]
y_shuffle = y[p]
#教師データ
X_train = X_shuffle[0:n_train_max,:]
Y_train = np.identity(n_classes)[y_shuffle[0:n_train_max]]
#検証データ
X_valid = X_shuffle[n_train_max:n_valid_max,:]
Y_valid = np.identity(n_classes)[y_shuffle[n_train_max:n_valid_max]]
#テストデータ
X_test = X_shuffle[n_valid_max:n_test_max,:]
Y_test = np.identity(n_classes)[y_shuffle[n_valid_max:n_test_max]]
return X_train,Y_train,X_valid,Y_valid,X_test,Y_test
引数のsize_ratioは３要素のタプルを想定しており、それぞれ教師データ、検証データ、テストデータのデータ全体から取得する比率を設定します。
例えば(0.6,0.2,0.2)ならば全体の60%,20%,20%を教師データ、検証データ、テストデータとして使用することになります。
内部ではデータの偏りがないように全体をシャッフルした後に分割します。（本当は分類クラスの数が均等になるように別ける方が良いのですが、今回はそこまでしませんでした。）
なお正解データはone-hot表現に変換しています。
実行
ここまで関数をいくつも実装してきましたが、ようやく実行です。
まずデータを分割します。
#MNISTデータの一部を取得
X_train,Y_train,X_valid,Y_valid,X_test,Y_test = get_split_data(mnist.data / 255, mnist.target.astype(int), (0.02,0.005,0.005))
データを分割する比率は(0.02,0.005,0.005)としています。
全体は70,000件なので教師データは1,400件、検証データは350件、テストデータは350件となります。
ロジスティック回帰での学習（最適化）を実行します。（学習率は0.1、繰り返し回数は1,000回としています。）
alpha = 0.1
iter_max = 1000
W,b = optimize(X_train, Y_train, X_valid, Y_valid, alpha, iter_max)既存のライブラリなどでは「ミニバッチ数」と「エポック数」を設定する事があると思いますが、今回はデータが多くないので、全てのデータを毎回の繰り返しで使ってます。（つまりミニバッチ数＝全教師データ数、エポック数＝繰り返し回数です。）
実行すると損失関数と精度が描画されます。
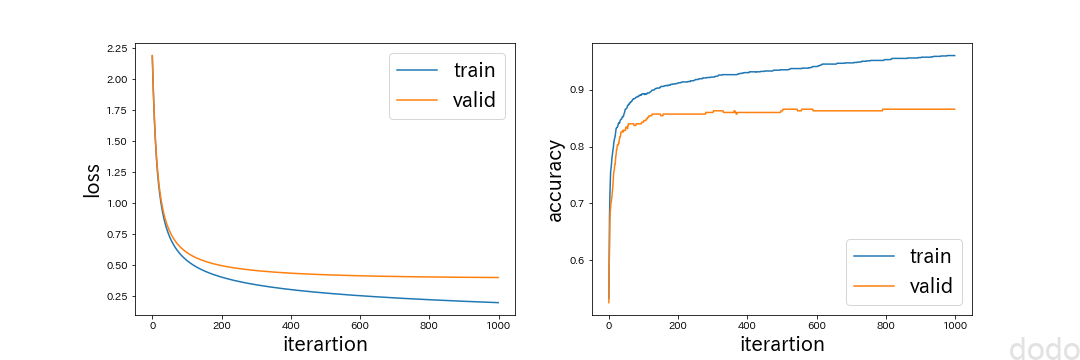損失関数と精度の回数毎の値このグラフから損失関数も精度も収束している事がわかります。
検証データの制度は85%程度となっています。
最後に最適化されたパラメータ(\(W,b\))を元にしてテストデータの精度を調べます。
Y_predict_proba = softmax(linear_trans(X_test,W,b))
print(get_accuracy(Y_test,Y_predict_proba))
結果は「0.9086」となりました。(小数点以下4桁で切っています。以降も同様。）
未知のデータに対して90%の精度を出せれば、なかなかのものではないでしょうか。
既存ライブラリとの比較
検証も兼ねて、いくつかの既存のライブラリを使ってロジスティック回帰を実行した場合の結果とスクラッチの結果を比較してみます。
データはスクラッチでやった場合と同じ教師データとテストデータを使用します。
LogisticRegression(sklearn)
まずは、sckit-learnのロジスティック回帰を使用します。
なおスクラッチで作成したものと同様に正則化はしないようにしています。(penalty=’none’で指定)
ただし最適化の方法については（普通の）最急降下法のオプションは無いようなので、デフデフォルトのLBFGS法というものを使用しています。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
estimator = LogisticRegression(penalty='none', random_state=0)
#one-hot表現ではないので元の数値表現に戻して計算する
estimator.fit(X_train,Y_train.argmax(axis=1))
Y_predict = estimator.predict(X_test)
accuracy_score(Y_test.argmax(axis=1),Y_predict)
テストデータの精度は、「0.8629」となりました。
最適化の方法が異なるので全く同じ結果にはなりません・・というかむしろこちらの方が結果が悪いですね・・
因みにpenaltyを指定しない場合（L2正則化をする場合）で計算すると・・・
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
estimator = LogisticRegression(max_iter = 1000, random_state=0)
estimator.fit(X_train,Y_train.argmax(axis=1))
Y_predict = estimator.predict(X_test)
accuracy_score(Y_test.argmax(axis=1),Y_predict)
テストデータの精度は、「0.9057」となりました。
MLPClassifier(sklearn)
LogisticRegression(sklearn)だとスクラッチで作成したロジスティック回帰と同じ方法（全データを毎回使用した場合の最急降下法）を指定できないので、同じsckit-learnのニューラルネットワークを使用して、隠れ層を０としてロジスティック回帰を実現します。
「solver=”sgd”」は「確率的勾配降下法」なので、全データを毎回使用した場合の最急降下法とは異なりますが、バッチサイズを教師データの件数とすれば、最急降下法と同じになるはずです。
以下ソースコードになります。
from sklearn.neural_network import MLPClassifier
estimator = MLPClassifier(max_iter=1000,
solver="sgd",
batch_size=X_train.shape[0],#バッチサイズは全データサイズ
learning_rate_init=0.1, #学習率0.1
hidden_layer_sizes=(), #隠れ層なし
alpha = 0, #正則化しない
momentum=0, #モメンタム法を使用しない
random_state=0)
estimator.fit(X_train,Y_train.argmax(axis=1))
Y_predict = estimator.predict(X_test)
accuracy_score(Y_test.argmax(axis=1),Y_predict)
テストデータの精度は、「0.8914」となり、スクラッチでやった結果と近い値になっています。(理屈では、全く同じ値になってもいいような気もしますが・・）
keras
最後はkerasを使用した場合です。
MLPClassifier(sklearn)と同様に、パラメータは、スクラッチの方法と同じになるように指定します。
なお収束具合を見るためにスクラッチの場合で実装した「plot_iteration」を使用しています。
import tensorflow as tf
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, input_shape=(784,)),
tf.keras.layers.Activation("softmax")
])
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
loss='categorical_crossentropy',
metrics=['accuracy'])
model.summary()
history = model.fit(X_train,
Y_train,
batch_size = X_train.shape[0],
validation_data = (X_valid,Y_valid),
epochs=1000,
verbose=0)
plot_iteration(history.history["loss"],
history.history["accuracy"],
history.history["val_loss"],
history.history["val_accuracy"])
model.evaluate(X_test, Y_test, verbose=2)
以下は実行結果の画面ダンプです。
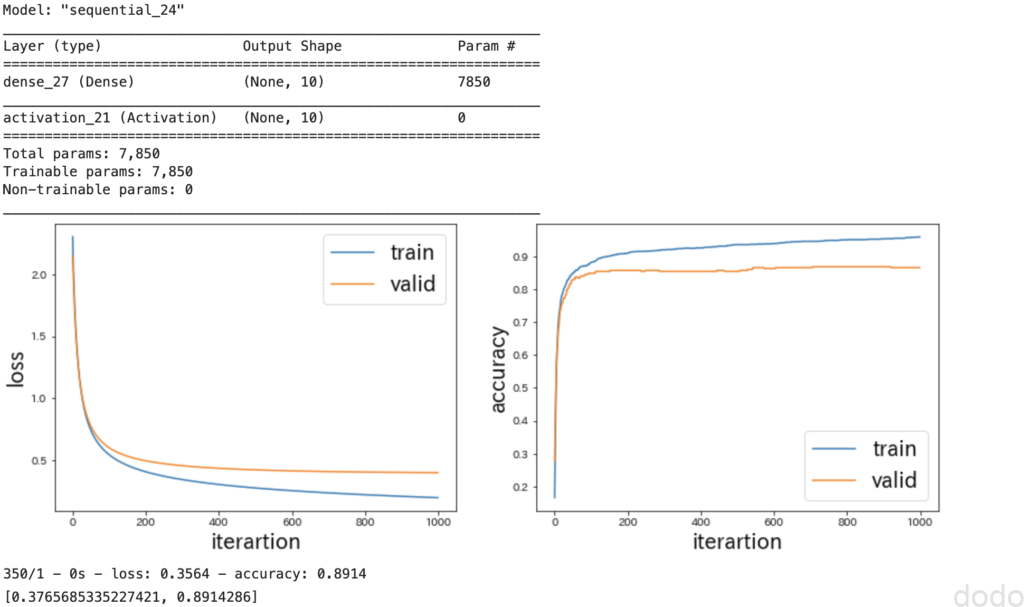kerasによるロジスティック回帰の実行結果
テストデータの精度は、「0.8914」となり、MLPClassifier(sklearn)と同じ値、そしてスクラッチでやった結果と近い値になっています。
MLPClassifier(sklearn)と同じ値になるなら、スクラッチの場合とも同じ値になって良さそうなものですが、深く追求しない事にします。。
まとめ
以上、ロジスティック回帰を１から実装してMNISTで性能を検証してみました。
たった1400程度の教師データで、こんな単純なモデルで9割に迫る性能が出れば、なかなかのものではないでしょうか？
これ以上の精度を求めるならば、モデルを複雑にすることももちろんですが、様々な最適化（データを増やす、データ加工、ハイパーパラメータの調整）が必要となるでしょう。
なお、もちろん実際の業務ではsckit-learnなどの既存のライブラリを使った方が良いことは言うまでもありません。（「車輪の再発明」をする必要はないので・・）
それでもスクラッチで実装するメリットとしては以下の事があげられます。
- 簡単なコードで機械学習が可能な事を実感できる。
- 機械学習の基本的な仕組みがわかる。
なので、一度、勉強がてら自分でやってみる事をお勧めします。
