第3週はいよいよ分類問題となり、最初のモデルとして「ロジスティック回帰」について説明されています。
・・というのをあまり今まで深く考えて来なかったですが、この講座でようやくしっくりきました。
本記事では、そのような事も含め「ロジスティック回帰」について、自分なりの解釈を交えてまとめていきます。
分類とは？
「回帰」は、ある特徴量から連続した値を予測するモデルでしたが、「分類」は「あり/なし」などのカテゴリーを予測するモデルです。
例えば、「メールの文面から、迷惑メールか普通のメールかを予測する」「腫瘍の大きさ・形などから、悪性かどうかを予測する」などなどを扱う問題が「分類」です。
回帰から分類へ
教師データからモデルを作成するには、予測したい値を数値として扱う必要があるため、「普通のメール=0」「迷惑メール=1」もしくは「良性腫瘍=0」「悪性腫瘍=1」というようにカテゴリーを数値に割り当てます。
その上で、まずは強引に「\(h_\theta(x) = \theta_0 + \theta_1 x\)」の関数で0と1の値を回帰してみます。（以後、簡単のためまずは単回帰で考えます。）
当然ですが、求められる\(h_\theta(x) \)は予測したい値（０もしくは１）とは限らずにいろんな値を取るので以下のようにその値が0.5以上かどうかによって、0か1かを決定するものとします。
\begin{eqnarray}y= \begin{cases} 1 & ( h_\theta(x) \geqq 0.5 ) \\ 0 & ( h_\theta(x) \lt 0.5 ) \end{cases}\end{eqnarray}
図で表すと以下の左が普通の回帰で、右が分類（無理やり直線で回帰）したものです。
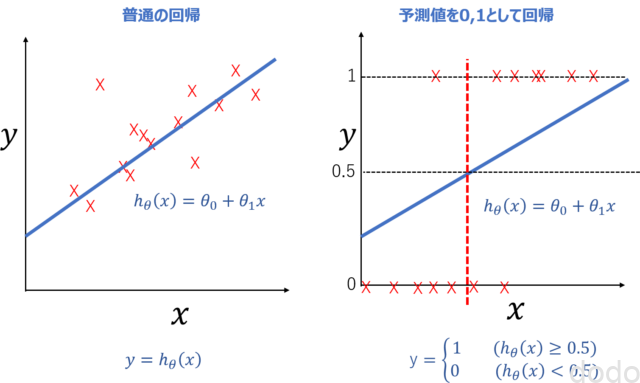予測値を0、1として回帰右図で赤い点線（厳密には、\(x\)のある値の”点”）が\(y\)が0か1の境界です。\(x\)がこの点より右側ならば\(y=1\)、左側ならば\(y=0\)です。
このように、予測値を0、１として無理やり回帰した上で、閾値(0.5)によって判別したものが「分類」の第一歩になります。
「第一歩」と言ったのは、このままだとモデルとしてまだ不都合があるからです。
上で\(x\)を腫瘍の大きさ、\(y\)を悪性かどうか（0ならば良性、1ならば悪性）とすると、データとして\(x\)が大きいもの（腫瘍が大きいもの）を用意すると、回帰する直線が、そのデータに引っ張られて、悪性かどうか(0か1か)の境界がずれてしまいます。
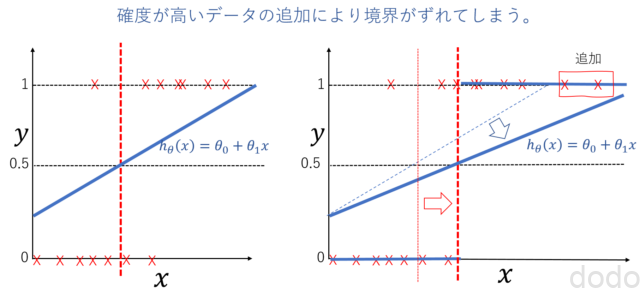角度の高いデータの追加により境界がずれる。（左図→右図）腫瘍が「めちゃくちゃ」大きい人のデータを用意したら、腫瘍が「まあまあ」大きい人が悪性から良性の判定に変わる・・・って変ですよね？
シグモイド関数
ではどうすれば良いかと言うと、回帰する関数をこれまでの線形関数から以下のような関数に変更します。
\begin{eqnarray}h_\theta(x) =& g(\theta_0 + \theta_1x) \\g(z) =& \dfrac{1}{1 + e^{-z}}\end{eqnarray}
ここで\(g(z)\)はシグモイド関数と呼ばれ以下ような特性があります。
- \(0 \leq g(z) \leq 1 \)
- \(z = 0 \Rightarrow g(z)=0.5 \)
- \(z \to \infty \Rightarrow g(z)=1 \)
- \(z \to -\infty \Rightarrow g(z)=0 \)
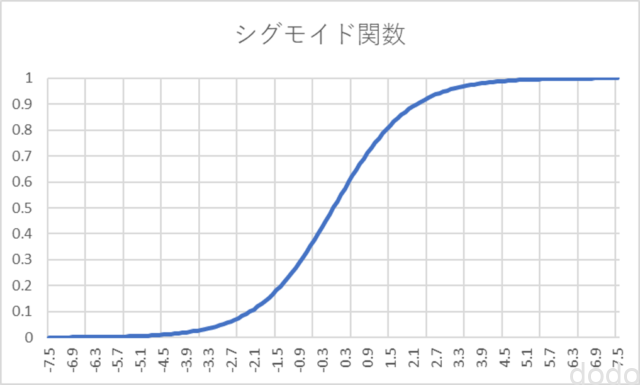シグモイド関数図で表すと、線形関数で回帰して分類してたものが左図、シグモイド関数（線形関数を引数としている）で回帰して分類したものが右図です。
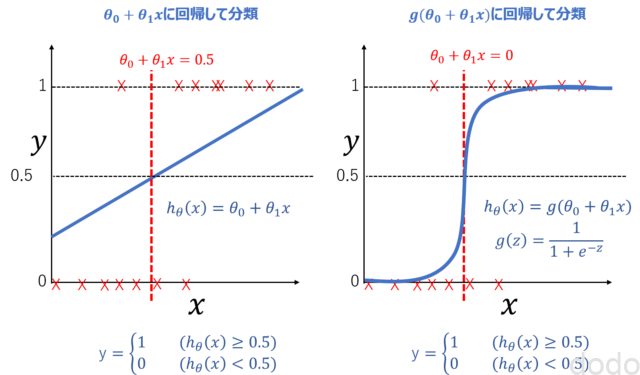シグモイド関数により回帰して分類シグモイド関数では、大きい値のデータの追加によって、境界がずれにくくなります。
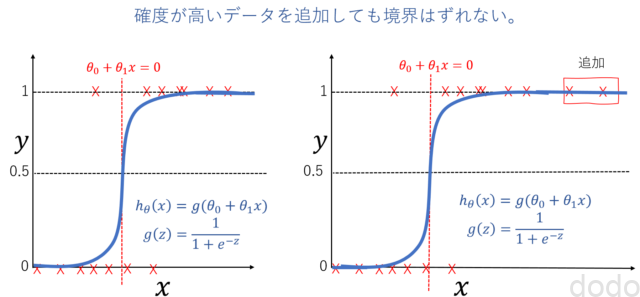データの追加で境界がずれないこのように線形関数を引数としたシグモイド関数により回帰することによって分類するモデルをロジスティック回帰と言います。
「回帰」と言う言葉に惑わされますが、「分類」の手段として「回帰」を使うだけで、やる事はあくまでも分類（あり/なし等を分ける）です。
これが最初に書いた「なんで分類なのに回帰って言うの？」の答えです。
なお、このシグモイド関数は、適当に良さげな関数を見つけてきて使っている訳ではありません。
数学的には、ベルヌーイ分布（０か１かどちらの結果が出るかの確率分布）と密接に関係があり、得られる出力\(h_\theta(x)\)の値はそのまま確率として解釈できます。（例えば、0.7ならば悪性腫瘍である確率が70%など・・）
なお、講座では、ベルヌーイ分布の話までは出てきません。メンターの人がフォーラムで「シグモイド関数は単に0から１の間になるってだけで確率とか意味してないよ。講義で確率って言ってるのは、数学とかにあまり詳しくない人に直感的にわかりやすく説明しているだけだよ」と回答してて、メンターあてにならんと思いました。（この後に出てくる多クラス分類でシグモイド関数使った場合は総和が１にならないから、そういう回答をしているっぽいですが・・）
決定境界
上の図の中でさらっと書いておりますが、ロジスティック回帰の場合、\(h_\theta(x)\)が0,5以上かどうかによって\(y\)が「0」か「1」かを分けるとすると、それを決定する境界は、\(\theta_0 + \theta_1 x =0\)です。(単に線形関数に回帰していた時は、\(\theta_0 + \theta_1 x =0.5\)でした。）
決定境界は、変数が１つならば「点」であり、変数が２つならば「線」であり、一般的には「超平面」です。
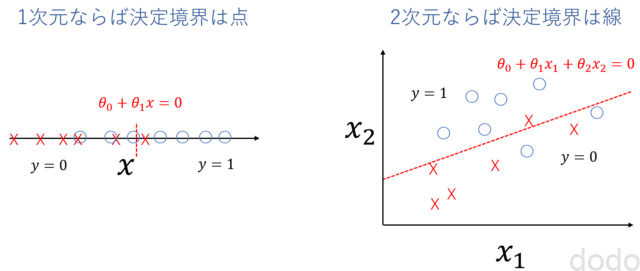決定境界第2週の受講記で定義した行列表現により以下のように表現できます。
\begin{align}& \theta^T x \geq 0 \Rightarrow y = 1 \newline& \theta^T x < 0 \Rightarrow y = 0 \newline\end{align}
ロジスティック回帰においては、\(y\)と\(x\)の関係は線形ではないですが、このように決定境界は線形の超平面になるので、線形モデルです。
なお、一般的には、決定境界自体は、線形である必要はなく、例えば\(\theta_0 + \theta_1 x_1^2+ \theta_2 x_2^2 =0\)などのようにすれば、非線形の円を境界とする事もできます。
目的関数
ロジスティック回帰の場合の目的関数は、どのようになるでしょうか？
線形回帰で使用していた目的関数\(J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2\)だと形が凸面にならずに、最小値が求められないとのことです。
なのでロジスティック回帰の場合は、うまく最初値が求められるような以下の目的関数を定義します。
$$J(\theta)=-\frac{1}{m}\sum_{i=1}^{m} y^{(i)}\log(h_\theta(x^{(i)})) + (1 – y^{(i)}) \log(1 – h_\theta(x^{(i)}))$$
講座内では、図を使って目的関数を決めることに時間を割いてますが、ここでは省略します。ただ\(y=1\)の場合は、\(h_\theta=1\)に近づくほど小さくなり、\(y=0\)の場合は、\(h_\theta=0\)に近づくほど小さくなる事がわかると思います。
なお、上記の目的関数を行列表現をすると以下のようになります。
$$J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(g(X\theta))-(1-y)^{T}\log(1-g(X\theta))\right)$$
そして目的関数を微分すると以下のようになり・・
$$\nabla J(\theta)=\frac{1}{m}X^{T}(g(X\theta)-\vec{y})$$
最急降下法により\(\theta\)を求める事ができます。
$$\theta:=\theta-\alpha \frac{1}{m}X^{T}(g(X\theta)-\vec{y})$$
ちなみに、上の式で単に線形回帰の時の\(X\theta\)が\(g(X\theta)\)に置き換わってるだけに見えるのは、シグモイド関数の場合、計算したら”たまたま”そうなっただけで、一般的にはそんなわけには行きません。（また線形関数微分は単純なので結構簡単に導出できますが、シグモイド関数の場合の微分計算は結構、複雑です。）
講座では、この後、唐突に最急降下法よりも高度な手法として、BFGS法と言うものを紹介しています。
紹介・・と言ってもその詳しい内容を紹介している訳ではなく、\(J(\theta) \)と\(\dfrac{\partial}{\partial \theta_j}J(\theta) \)を求められれば、OctaveにBFGS使えるライブラリがあるので、最急降下法よりも便利だよ・・と言うことです。（αとか決める必要なくて便利なので実際に演習では、そっちを使います。）
BFGS法自体を詳しく説明している訳ではないので、本記事では、この程度の記載に留めます。
多クラス分類
ここまで記載してきた分類は、２部類（０または1)でしたが、複数のカテゴリーに分離した場合は、どうすれば良いでしょうか？
いくつか方法があるようですが、講座では、One-vs-all(1対他）と言う方法を紹介してます。
例えば3つのカテゴリーに分類したい場合、それぞれをクラス0、クラス1、クラス2として、まずは、クラス0とそれ以外を分類するためのモデルを考えて、ロジスティック回帰により\(h_\theta^{0}(x)\)を求めます。
そして同様にクラス1とそれ以外を分類するモデル\(h_\theta^{1}(x)\)、クラス2とそれ以外を分類するモデル\(h_\theta^{2}(x)\)を求めます。
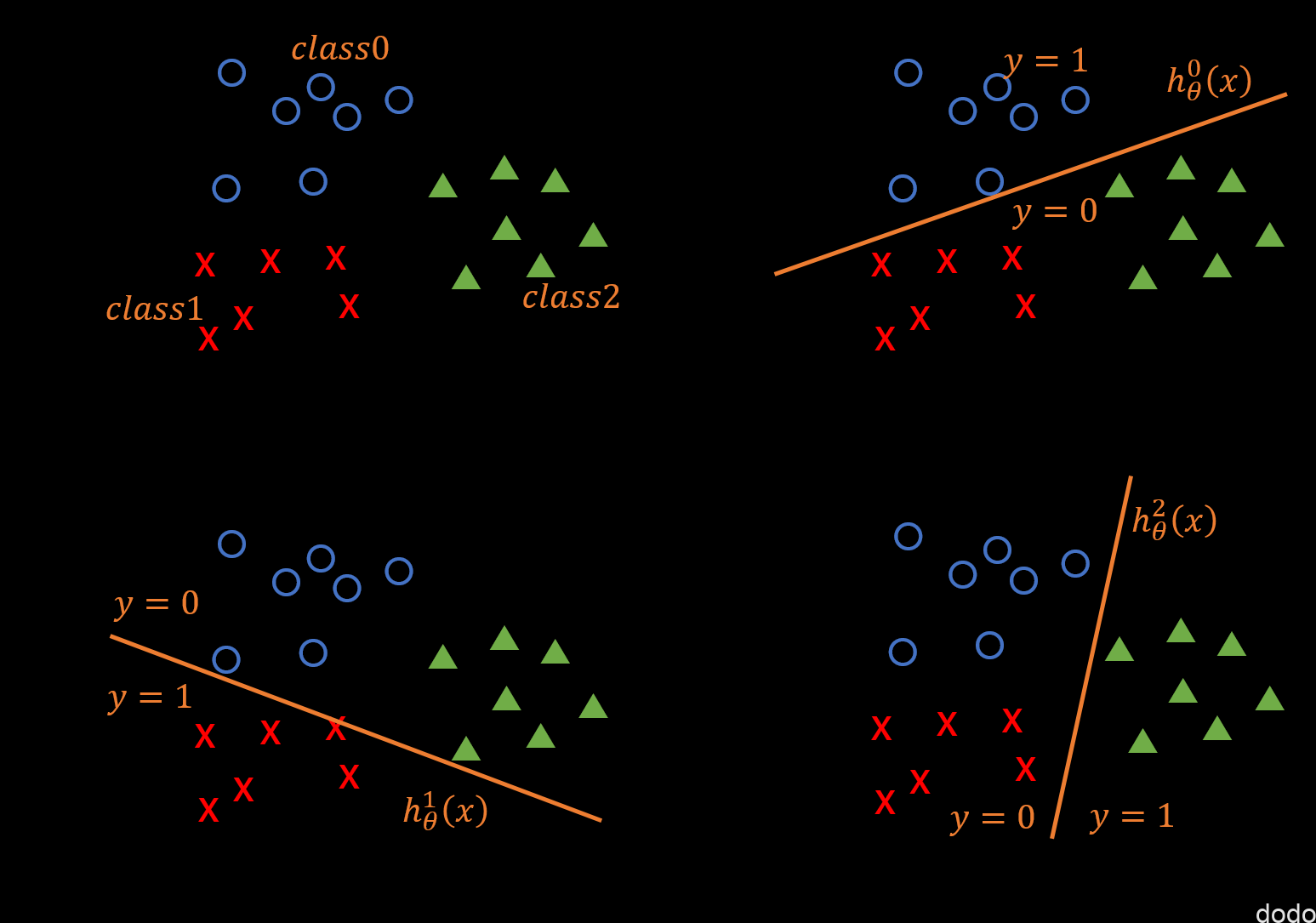多クラス分類（１対他）例えば、予測したいデータを\(h_\theta^{0}(x)\)、\(h_\theta^{1}(x)\)、\(h_\theta^{2}(x)\)に入力した時に、それぞれの値が、0.4、0.6、0.1だったとすると、クラス１に属する確率が0.6で一番大きい事になり、そのデータはクラス１に属すると判定します。
上でちょっと触れましたが、一つ一つの出力は確率を意味しますが、各クラスに属する確率は別々のモデル（\(h_\theta^{0}(x)\)、\(h_\theta^{1}(x)\)、\(h_\theta^{2}(x)\)）の結果なので足しても１にはなりません。足して１になるようにする（確率として解釈できるようにする）にはシグモイド関数を拡張したソフトマックス関数というものを使います。
まとめ
本記事では、Coursera機械学習の第3週目の前半のロジスティック回帰の内容についてまとめました。
講座でわかりやすいと思ったのが「回帰から分類への流れ」です。
いきなりシグモイド関数が出てくるよりも線形回帰からの流れでどうしてそれが必要なのか説明されているため、わかりやすかったです。
次回は、第3週の後半の正則化について書いていこうと思います。
