Processing math: 100%
データ分析 PR

Pythonのstatsmodelsを利用した時系列分析事始め

  /
時系列解析(statsmodels)
記事内に商品プロモーションを含む場合があります

Pythonのstatsmodelsというパッケージを使うとサクッと時系列データから、自己相関、トレンド、季節性などを抽出することができます。

本記事では、statsmodelsを使って、適当に作ったテストデータからトレンドを抽出する方法について記載します。

サイン波

まずは普通のサイン波について解析してみます。

必要なパッケージをインポートします。

import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
%matplotlib inline
Python

 

サイン波そのものをプロットしてみましょう。

def normal_plot(data,filename):
    fig, ax = plt.subplots(figsize=(10, 5)) 
    ax.plot(data)
    plt.savefig(filename,bbox_inches='tight', pad_inches=0.2)
    plt.show()

sample_data = np.sin(np.arange(0,200) * np.pi/5)
normal_plot(sample_data,"./sample_seasonal_statics.png")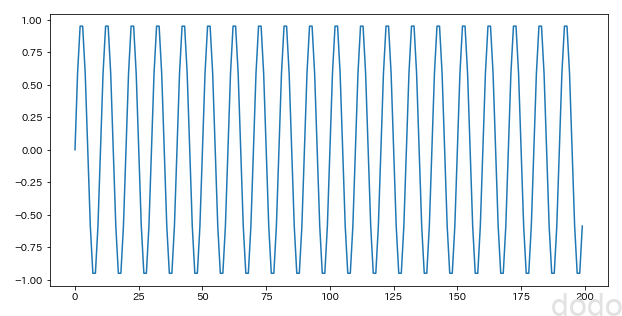
Python
サンプル１:サイン波サイン波

グラフ見ただけで周期性があるのは明らかですが、その周期がいくつなのかが、一見わかりづらいです。（目盛りを増やせばわかるかもしれませんが・・）

次に、このサイン波の自己相関・偏自己相関を見てみます。

def correlation_plot(data,filename):
    fig = plt.figure(figsize=(10,8))
    # 自己相関のコレログラム
    ax1 = fig.add_subplot(2,1,1)
    ax1.set_ylim(-1,1)
    fig = sm.graphics.tsa.plot_acf(data, lags=40, ax=ax1)
    # 偏自己相関のコレログラム
    ax2 = fig.add_subplot(2,1,2)
    ax2.set_ylim(-1,1)    
    fig = sm.graphics.tsa.plot_pacf(data, lags=40, ax=ax2)
    plt.savefig(filename,bbox_inches='tight', pad_inches=0.2)
    plt.show()

correlation_plot(sample_data,"./sample_seasonal_correlation_statics.png")
Python

ここでstatsmodelsパッケージの「graphics.tsa.plot_acf」「graphics.tsa.plot_pacf」を利用します。これらの関数の戻り値は、データ自体ではなく、matplotlibのfigureインスタンスとなります。

引数で指定されているlagsは「ラグ数」といって元のデータからどれだけずらした量かを表します。ここでは40までずらしたところまでプロットさせています。

実行結果は以下のようになります。

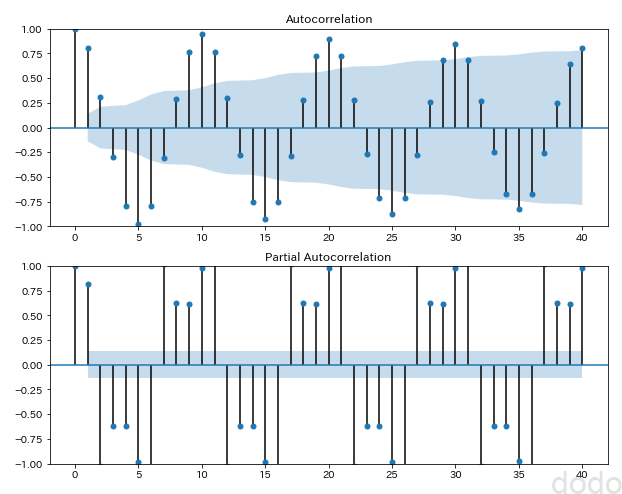サンプル１：サイン波（自己相関）サイン波（自己相関）

図の上が自己相関、下が偏自己相関です。色が塗られている部分は95%信頼区間で、この範囲内だと「相関はない」という帰無仮説が棄却されない事を意味します。

つまりその範囲を超えていれば、帰無仮説が棄却されて、相関があると言えます。

帰無仮説が棄却されないと言う事は、帰無仮説が正しいということではありません。グラフの色塗りの箇所の範囲内の場合は「相関がない」ではなく「相関があるとは言い切れない」ということになります。

なお、偏自己相関は、途中の相関を見る点の間の点の影響と除去したものとなります。(例えば、t1とt5の間の相関を見る時にt2,t3,t4の影響を除去します。）

サイン波の場合、自己相関を見ると10ずれるごとに相関が強く出ており、10の期間で周期性がある事がわかります。

※スケールの上限を1としてますが、偏自己相関は上限が１におさまらないケースがあるようです。（実は11ずれた箇所はグラフを飛び抜けて40くらいの値になっています。これについては、よくわかりません。。理由がわかったら追記します。）

10の周期がある事がわかったので、「seasonal_decompose」を使用してこの時系列データを「トレンド」「季節性」「残差」に分解します。（以降、「周期性」を「季節性」と記載します。）

def seasonal_decompose_plot(data,freq,filename):
    res = sm.tsa.seasonal_decompose(data, freq=freq)
    fig = res.plot()
    fig.set_size_inches(8.5,10)
    fig.tight_layout()
    plt.savefig(filename,bbox_inches='tight', pad_inches=0.2)
    plt.show()
    
seasonal_decompose_plot(sample_data,10,"./sample_seasonal_decompose_statics.png")
Python

引数のfreqは、周期を表します。10の周期がある事がわかっているので、10を指定しています。

実行結果は以下のようになります。

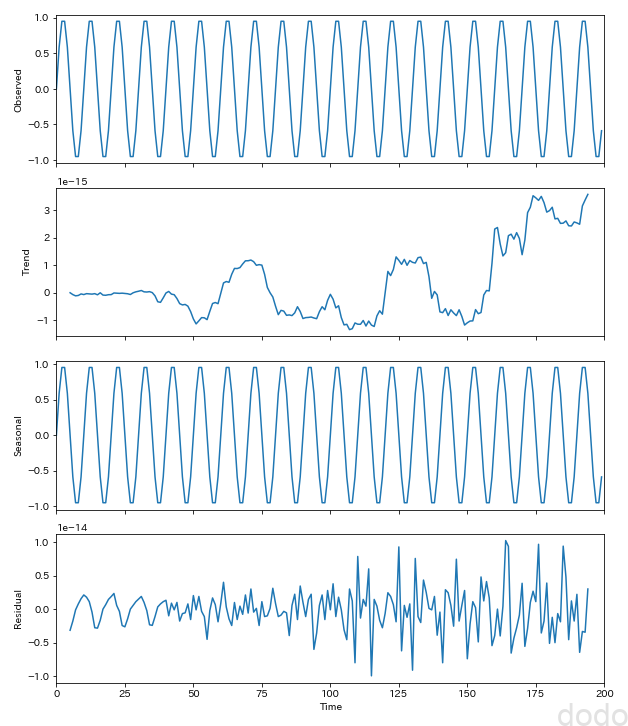サンプル１：サイン波（トレンド））サイン波（トレンド）

上から「元のデータ」「トレンド」「季節性」「残差」がプロットされています。

スケールを見るとわかりますが（グラフの左上にちらっと1e-15とか書かれてます）、サイン波の場合、「トレンド」と「残差」はほぼ０です。

なので当たり前ですが、サイン波から季節性を取ったら何も残りません。

サイン波+1次間数

次にサイン波に”傾き”を追加してみます。（以降、サイン波の場合で定義済みの関数を使用します。）

sample_data_linear = np.sin(np.arange(0,200)*np.pi/5) + np.arange(0,200) /20

normal_plot(sample_data_linear,"./sample_seasonal_linear.png")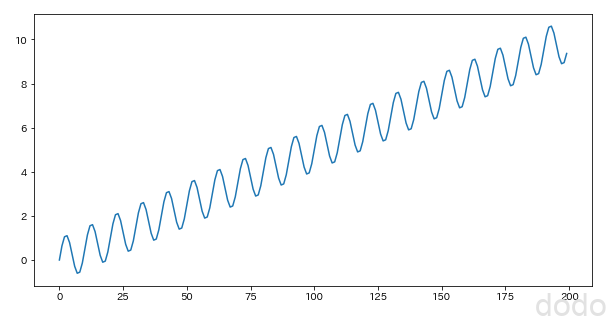
Python
サンプル２：サイン波＋１次間数サイン波＋１次間数

まずは、自己相関をみてみます。

correlation_plot(sample_data_linear,"./sample_seasonal_correation_linear.png")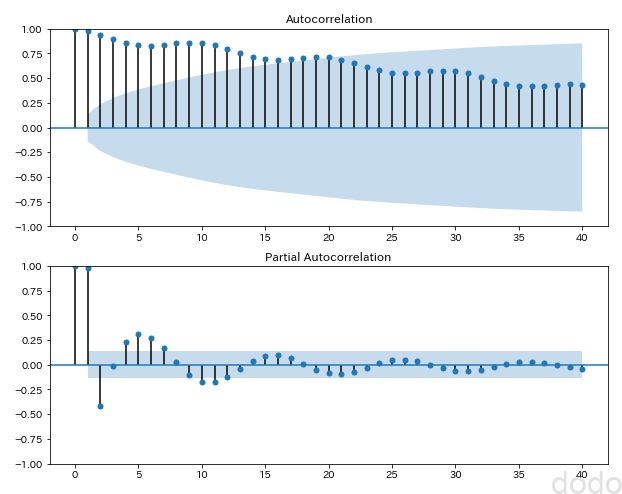
Python
サンプル２：サイン波＋１次間数（自己相関）サイン波＋１次間数（自己相関）

自己相関も偏自己相関も時系列の差が大きくなるほど相関は小さくなりますが、かろうじて10ごとの周期を見ることができます。

では、10を周期としてトレンド・季節性・残差を見てみましょう。

seasonal_decompose_plot(sample_data_linear,10,"./sample_seasonal_decompose_linear.png")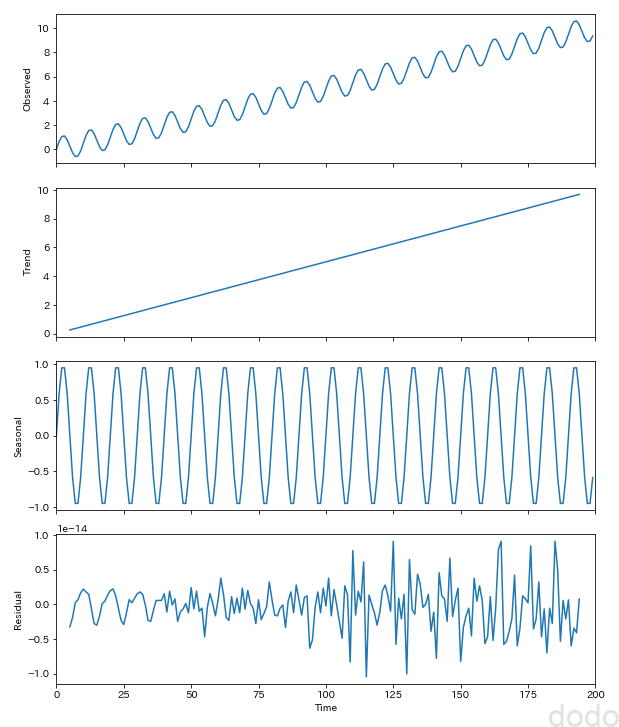
Python
サンプル２：サイン波＋１次関数（トレンド）サンプル２：サイン波＋１次関数（トレンド）

トレンドとして１次関数の上昇傾向が抽出されています。

サイン波+1次間数+ノイズ

サイン波＋１次関数にさらに乱数でノイズを追加した場合について解析します。

sample_data_noisy = np.sin(np.arange(0,200)*np.pi/5) \
                  + np.arange(0,200) /20 \
                 - np.random.random_sample(200)

normal_plot(sample_data_noisy,"./sample_seasonal_noisy.png")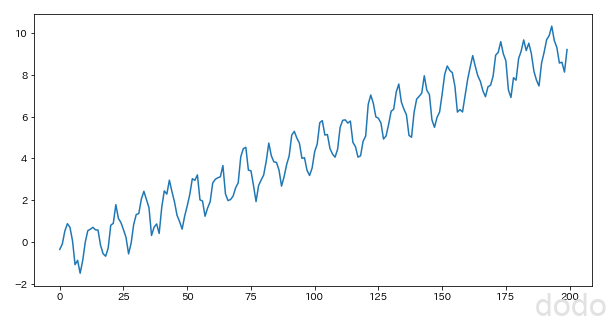
Python
サイン波＋１次間数＋ノイズサイン波＋１次間数＋ノイズ

自己相関は以下のようになります。

correlation_plot(sample_data_noisy,"./sample_seasonal_correation_noisy.png")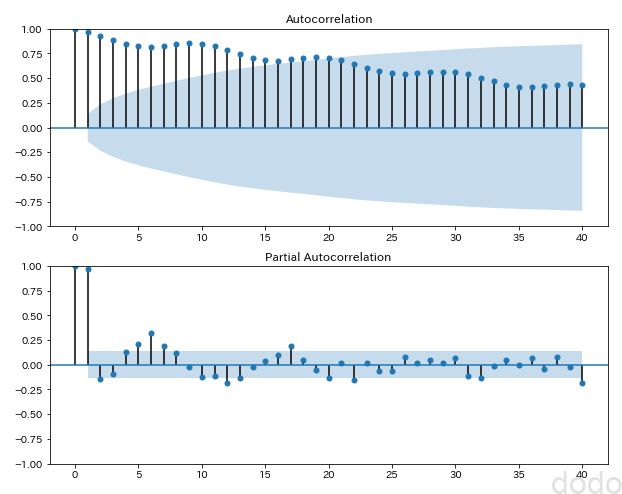
Python
サイン波＋１次間数＋ノイズ（自己相関）サイン波＋１次間数＋ノイズ（自己相関）

ノイズを入れない場合とあまり大差がないように見えます。やはり辛うじて、10ごとの周期が見られるようです。

では、10を周期としてトレンド・季節性・残差を見てみましょう。

seasonal_decompose_plot(sample_data_noisy,10,"./sample_seasonal_decompose_noisy.png")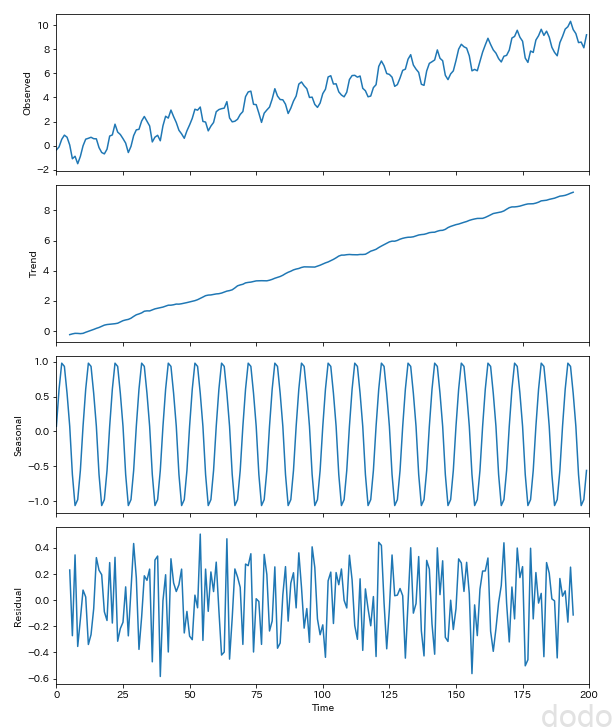
Python
サイン波＋１次間数＋ノイズ（トレンド）サイン波＋１次間数＋ノイズ（トレンド）

ノイズがある分、多少はガタついてますが、トレンドもちゃんと抽出できているようです。またこれまでは残差は無視できるほど小さかったですが、ノイズの分、残差は大きくなっています。

まとめ

以上、３パターンのテストデータで、statsmodelsを使って時系列の分析をしてみました。

簡単、かつ結果がわかりきっているデータではありますが、まずは使い方についてイメージしていただければ幸いです。

機会があれば、実データを用いてstatsmodelsを使ってデータを分析してみたいと思います。

 

こんな記事もおすすめ