母集団から標本（\(X_1,\cdots,X_n\)）を取得したとき、その平均の期待値は、母平均（\(\mu\)）に一致します。
\begin{eqnarray}
E\left(\frac{X_1+\cdots+X_n}{n}\right) &=&\mu\\
\end{eqnarray}
一方、標本分散の期待値は、母分散（\(\sigma^2\)）に一致しません。
\begin{eqnarray}
E\left(\frac{(X_1-\bar{X})^2+\cdots+(X_n-\bar{X})^2}{n}\right) &\neq&\sigma^2\qquad (\bar{X}=\frac{X_1+\cdots+X_n}{n})\\
\end{eqnarray}
母分散（\(\sigma^2\)）に一致するのは、以下の不偏分散の期待値となります。
\begin{eqnarray}
E\left(\frac{(X_1-\bar{X})^2+\cdots+(X_n-\bar{X})^2}{\color{red}{n-1}}\right) &=&\sigma^2\qquad (\bar{X}=\frac{X_1+\cdots+X_n}{n})\\
\end{eqnarray}
最初、なぜ、\(n\)ではなく\(n-1\)で割るのかピンと来ませんでした。
検索すれば、自由度への言及からの直感的な説明や、数式による証明が見つかるでしょう。
それらを見れば、ある程度は納得できるのですが、やはり実際のデータで確かめてみたいものです。
本記事では、実際に母集団から標本データを取得して、その不偏分散の期待値が母分散に一致するのか確かめてみます。
不偏分散の検証
前提条件
本ソースコードは、Python3.10.3で起動するJupyter Lab上で実行されています。
また使用している各ライブラリのバージョンは以下の通りです。
- numpy(1.22.4)
- scipy(1.8,1)
- matplotlib(3.5.2)
- seaborn(0.11.2)
可視化の準備
今回は可視化のためにmatplotlib+seabonを使用します。
文字フォント、文字の大きさなどについて以下のように設定します。
import matplotlib.pyplot as plt
import seaborn as sns
#図形のサイズ
plt.rcParams["figure.figsize"] = (10, 6)
#フォントの大きさ
plt.rcParams["font.size"] = 15
#使用フォント
sns.set(font='Hiragino Sans')母集団を生成して標本を取得
母集団を生成して標本を取得します。
母集団は、\(X \sim N(10,3^2)\) （平均10、標準偏差3の正規分布）に従う1万件のデータとします。
from scipy import stats
parent_set_normal = stats.norm.rvs(loc=10, scale=3, size=10000)
まずは試しに、標本サイズ５の標本を取得します。
import random
def get_sample(parent_set,sample_size):
"""
標本を取得する。
Parameters
----------
parent_set : ndarray
母集団のデータ
sample_size : int
標本サイズ
Returns
-------
sample : ndarray
標本データ
"""
indexes = random.sample(range(parent_set.size), k=sample_size)
return parent_set[indexes]sample = get_sample(parent_set_normal,5)
この標本の標本平均、標本分散、不偏分散を求めます。
numpyには、すでにそれらを求めるメソッドが用意されておりますが、本記事では何をやっているのかを見えやすくするため、あえて、それぞれを求める関数を作成します。
def mean(data):
"""
平均を求める。
Parameters
----------
data : ndarray
データ
"""
return np.sum(data) / len(data)
def var(data):
"""
分散を求める。
Parameters
----------
data : ndarray
データ
"""
return sum(np.square(data - mean(data))) / len(data)
def uvar(data):
"""
標本の場合の不偏分散を求める。
Parameters
----------
data : ndarray
データ
"""
return sum(np.square(data - mean(data))) / (len(data) - 1)
以下、numpyのメソッドの結果と比較すると同じ結果になっていることが確認できます。
print(f'平均 library: {sample.mean()} origin: {mean(sample)}')
print(f'分散 library: {sample.var()} origin: {var(sample)}')
print(f'不偏分散 library: {sample.var(ddof=1)} origin: {uvar(sample)}')実行結果 平均 library: 11.275296499755767 origin: 11.275296499755767 分散 library: 1.3116337472495256 origin: 1.3116337472495256 不偏分散 library: 1.639542184061907 origin: 1.639542184061907
母集団との比較
標本平均の期待値と母平均、標本分散・不偏分散の期待値と母分散を比べてみましょう。
まず標本サイズ５の標本を、100個取得します。
samples = [get_sample(parent_set_normal,5) for _ in range(100)]
それぞれの標本平均を求めます。
sample_mean = np.array([mean(sample) for sample in samples])
標本平均のヒストグラムと期待値、母平均を可視化します。
plt.hist(sample_mean, 30, density=True, alpha=0.7)
plt.axvline(mean(parent_set_normal),color='red', label=f'{mean(parent_set_normal):.2f}(母集団平均)')
plt.axvline(mean(sample_mean), color='blue', label=f'{mean(sample_mean):.2f}(標本平均の期待値)')
plt.legend(loc='upper right')
plt.tight_layout()
plt.savefig('sample_mean.jpg', dpi=100)それぞれの標本の出現確率を一様として、期待値を平均として求めます。（以後、分散の期待値も同様です。）
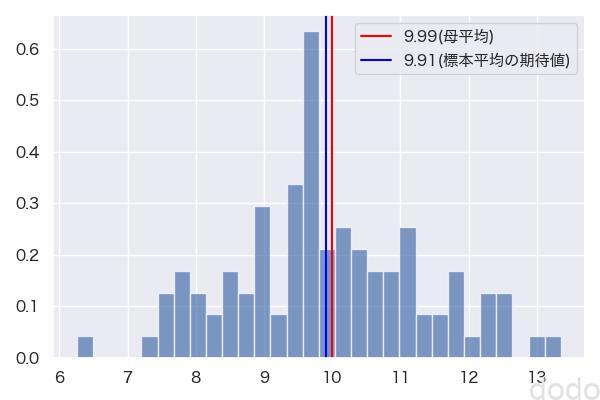標本平均VS母平均標本サイズ5、標本数100と、決して大きい数ではありませんが、標本平均の期待値と母平均が大体一致していることがわかります。
次に標本分散を求めます。
sample_var = np.array([var(sample) for sample in samples])
標本分散のヒストグラムと期待値、母分散を可視化します。
plt.hist(sample_var, 30, density=True, alpha=0.7)
plt.axvline(var(parent_set_normal),color='red', label=f'{var(parent_set_normal):.2f}(母分散)')
plt.axvline(mean(sample_var),color='blue', label=f'{mean(sample_var):.2f}(標本分散の期待値)')
plt.legend(loc='upper right')
plt.tight_layout()
plt.savefig('sample_var.jpg', dpi=100)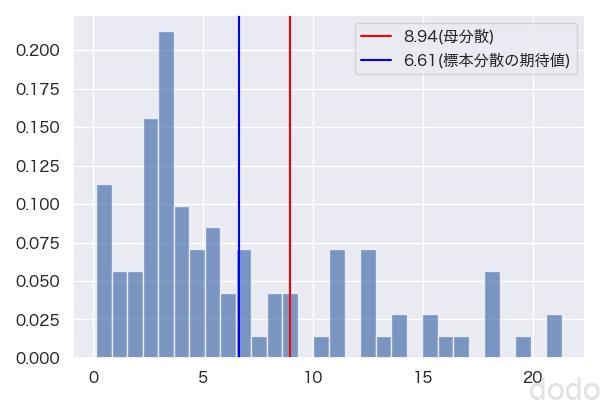
標本分散VS母分散標本分散と母分散はかなりずれていることがわかります。
では、不偏分散ならば、どうでしょう？
以下、不偏分散を求めます。
sample_uvar = np.array([uvar(sample) for sample in samples])
不偏分散のヒストグラムと期待値、母分散を可視化します。
plt.hist(sample_var, 30, density=True, alpha=0.7)
plt.axvline(var(parent_set_normal),color='red', label=f'{var(parent_set_normal):.2f}(母分散)')
plt.axvline(mean(sample_uvar),color='blue', label=f'{mean(sample_uvar):.2f}(不偏分散の期待値)')
plt.legend(loc='upper right')
plt.tight_layout()
plt.savefig('sample_uvar.jpg', dpi=100)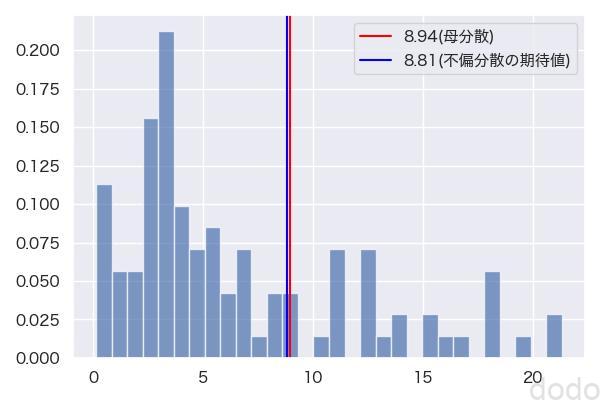
不偏分散VS母分散不偏分散の期待値は、かなり母分散と近い値になっている事がわかります。
標本数を変えて確認
上記の結果から、実際のデータで標本分散ではなく不偏分散の期待値が母分散に一致するのがわかると思います。
上記は標本数100固定でやりましたが、標本数がもっと少ない場合、多い場合にどうなるかを確かめてみましょう。
取得する標本数で比較できるように以下のように関数化します。
def plot_compare_sample_parent_stats(parent_set, params, file_name):
"""
母集団と標本の統計量を比較して描写する。
Parameters
----------
parent_set : ndarray
母集団のデータ
params : list[(int,int)]
(標本サイズ、標本数） を要素にもつリスト
file_name : str
保存ファイル名
"""
#figureサイズ
fig = plt.figure(figsize=(20,len(params)*5))
#母集団の求める統計量(平均、分散、分散)の関数とラベル
parent_stat_func = [mean, var, var]
parent_stat_label = ['母平均', '母分散', '母分散']
#標本の求める統計量(平均、分散、不偏分散）の関数とラベル
sample_stat_func = [mean, var, uvar]
sample_stat_label = ['標本平均', '標本分散', '不偏分散']
#描写する統計量の種類の数
stat_size = len(parent_stat_label)
#subfigure取得
subfigs = fig.subfigures(len(params))
for s,param in enumerate(params):
#標本取得
samples = [get_sample(parent_set,param[0]) for _ in range(param[1])]
#subfigureのタイトル設定
subfig = subfigs[s]
subfig.suptitle(f'標本サイズ{param[0]},標本数{param[1]}' ,fontsize=15)
#平均、分散、不偏分散のループ
for i in range(stat_size):
ax = subfig.add_subplot(1,stat_size,i+1)
#タイトル
ax.set_title(f'{sample_stat_label[i]}ヒストグラム')
#データのラベル
labels = (f'{sample_stat_label[i]}のヒストグラム',
parent_stat_label[i],
f'{sample_stat_label[i]}の期待値')
#母分散統計量
parent_stat = parent_stat_func[i](parent_set)
#標本統計量
sample_stat_array = np.array(
[sample_stat_func[i](sample) for sample in samples])
#標本統計量のヒストグラム
ax.hist(sample_stat_array, 30, density=True,
alpha=0.7, label=labels[0])
#標本統計量の期待値
ax.axvline(mean(sample_stat_array),
color='blue',
label=f'{mean(sample_stat_array):.2f}({labels[2]})')
#母集団統計量の値
ax.axvline(parent_stat,
color='red',
label=f'{parent_stat:.2f}({labels[1]})')
ax.legend(loc='upper right')
plt.savefig(file_name, dpi=100, bbox_inches='tight')
詳細は、コード内のコメントをご参照ください。処理を共通化しただけで、やっている内容は標本を取得して、標本平均、標本分散、不偏分散を求めて可視化しているだけです。
では、上記の関数を使用して、正規分布の母集団から標本サイズ５で固定して、標本数を5,10,50,100,500,1000と増やしていった場合に標本平均、標本分散、不偏分散がどのようになるか確かめてみましょう。
params = [(5,5),(5,10),(5,50),(5,100),(5,500),(5,1000)]
parent_set_normal = stats.norm.rvs(loc=10, scale=3, size=10000)
plot_compare_sample_parent_stats(parent_set_normal,
params,
'compare_sample_parent_stats_norm.jpg')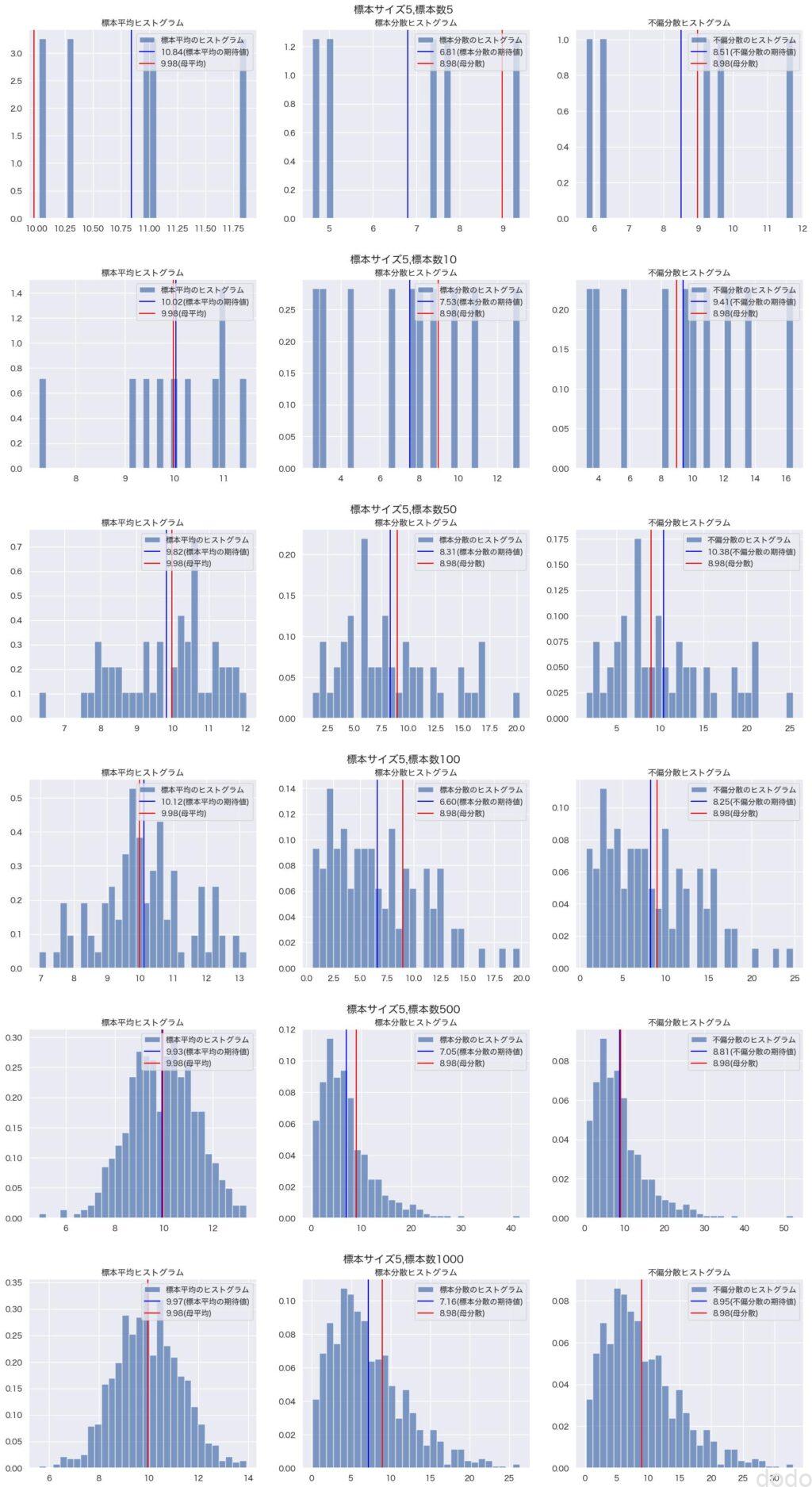
標本と母集団の平均・分散の比較（正規分布）標本数を増やすにつれて、標本平均と不偏分散の期待値はそれぞれ母平均と母分散に近づきますが、標本分散の期待値は母分散とずれた値のままになっているのがわかります。
ここまで正規分布の母集団についてやってきましたが、他の分布でも試してみましょう。
一様分布の母集団から標本サイズ５で固定して、標本数を5,10,50,100,500,1000と増やしていった場合に標本平均、標本分散、不偏分散がどのようになるか確かます。
params = [(5,5),(5,10),(5,50),(5,100),(5,500),(5,1000)]
parent_set_uniform = stats.uniform.rvs(loc=10, scale=3, size=10000)
plot_compare_sample_parent_stats(parent_set_uniform,
params,
'compare_sample_parent_stats_uniform.jpg')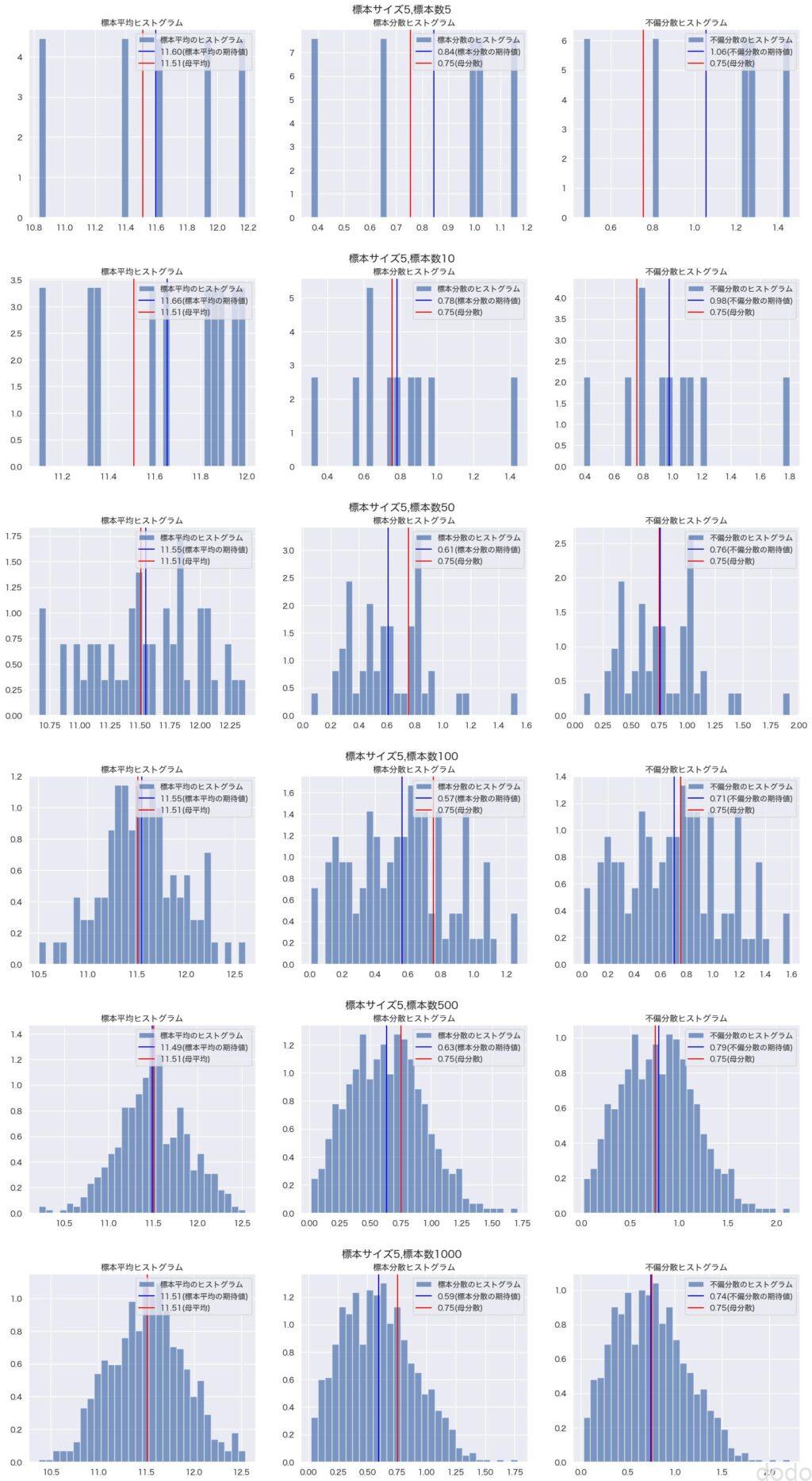
標本と母集団の平均・分散の比較（一様分布）一様分布が母集団の場合でも、標本数を増やすにつれて標本平均と不偏分散の期待値はそれぞれ母平均と母分散に近づき、標本分散の期待値は母分散とずれた値のままになっているのがわかります。
まとめ
以上、不偏分散の期待値が母分散に一致することを実際のデータを使って確かめてみました。
なお、この不偏分散については、以下の２つの話題（中心極限定理、信頼区間）とあわせて、私が最初に勉強したときに、今ひとつピンと来なかった話題となります。
同じような方がいたときに、これらの記事が何かしらの参考になれば幸いです。
