SIRモデルは感染症の流行を記述するための古典的な数理モデルです。
古典的ではありますが、新型コロナについてクラスター対策班がシミュレーションしているモデルもこのSIRモデルがベースとなっているようです。
またkaggleでも、このSIRモデルを使用して予測をしている人が何人かいます。
モデル自体は非常に単純なモデルのようなので試しにPythonで実装してみることにしました。
なお、本記事の目的はPythonで数理モデルを実装する事であり、決して現在の新型コロナの流行の予測を（真面目に）試みるものではありませんのでご注意ください。（パラメータとか適当に決めてますし、パラメータ次第で結果はどうにでもなります。）
SIRモデルとは？
SIRモデルについて簡単に説明します。
SIRモデルは、人口を、\(S\)（感受性保持者）、\(I\)（感染者）、\(R\)（免疫保持者）に分けた場合に\(S\)、\(I\)、\(R\)の人数がどのように変化していくかを時間変化の連立微分方程式で表現したものです。
\(S\)、\(I\)、\(R\)の連立微分方程式は以下のようになります。
\begin{eqnarray}
\frac{dS(t)}{dt} &=&-\beta S(t) I(t)\\
\frac{dI(t)}{dt} &=&\beta S(t) I(t) – \gamma I(t)\\
\frac{dR(t)}{dt} &=&\gamma I(t)\\
\end{eqnarray}
ここで\(\beta\)は感染率、\(\gamma\)は回復率（逆数は平均感染期間）を意味します。
フローで表すと\(S\)から\(I\)へ、\(I\)から\(R\)へ以下のようになります。
$$\Large S\,\overset{\beta I}{\rightarrow}\,I\,\overset{\gamma}{\rightarrow}\,R$$
この方程式を解く事によって、時間毎の\(S\)（感受性保持者）、\(I\)（感染者）、\(R\)（免疫保持者）を求める事ができます。
ここで、\(S\)、\(I\)の初期値を\(S_{0}\)、\(I_{0}\)とした場合、
$$\frac{dI(0)}{dt} =I_{0} (\beta S_{0} – \gamma)$$
となります。
\(\frac{dI(0)}{dt}>0\)の場合、つまり\(\frac{\beta S_{0}}{\gamma} > 1\)の場合に、感染が拡大することから、以下の\(\mathcal{R_{0}}\)を基本再生産数(1より大きい場合に感染が拡大にする）と定義します。
$$\mathcal{R_{0}} = \frac{\beta S_{0}}{\gamma} $$
基本生産数は、1人が感染させる人数というように解釈する事ができます。
本モデルの前提条件として全体の人口(\(S+I+R\))は常に一定で流入、誕生、死亡もないものとします。（感染による死亡者は\(R\)（免疫保持者）に混ぜて\(R\)（除去者）とする場合もあります。）
SIRモデルの実装
それではSIRモデルを実装して可視化してみましょう。
まずは必要なパッケージをインポートします。
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
%matplotlib inline
SIRモデルの常微分方程式を解くのは、自分でルンゲクッタ法などを実装してもそれほど難しくはないですが、ここでは、scipyパッケージのsolve_ivpという関数を使用します。
scipyにはodeintという関数があり、正直、こちらの方が使い勝手が良いのですが、odeintは廃止予定との事で、solve_ivpを使用します。
solve_ivpには、以下のようなcallback関数を渡せば良いのですが・・
def SIR(t, y):
dSdt = -beta * y[0] * y[1]
dIdt = beta * y[0] *y[1] - gamma * y[1]
dRdt = gamma * y[1]
return [dSdt, dIdt, dRdt]
パラメータを外から渡せる仕組みになっていないので、関数内関数を定義して使用します。
def SIR_wrapper(beta, gamma):
def SIR(t, y):
dSdt = -beta * y[0] * y[1]
dIdt = beta * y[0] *y[1] - gamma * y[1]
dRdt = gamma * y[1]
return [dSdt, dIdt, dRdt]
return SIR
この関数を呼び出してSIRの方程式を解きます。
ここでは、全人口を1000人として、感受性保持者の初期値を999人、感染者の初期値を1人とし、感染率（\(\beta\)）、回復率（\(\gamma\)）はそれぞれ0.0002、0.1とします。（この時の基本再生産数\(\mathcal{R_{0}}\)は1.998となります。）
#トレース時間
T = 160
#感受性保持者初期値
S_0=999
#感染者初期値
I_0=1
#免疫保持者初期値
R_0=0
beta, gamma = 0.0002, 0.1
result = solve_ivp(SIR_wrapper(beta, gamma), [0, T], [S_0, I_0, R_0], t_eval=np.arange(0, T))
#plot
fig = plt.figure(figsize=(10, 5))
plt.xlabel("日数",fontsize=15)
plt.ylabel("人数",fontsize=15)
plt.plot(result.t,result.y.T)
plt.legend(['感受性保持者','感染者', '免疫保持者'])
plt.savefig("./SIR_sample.png")
plt.show()
時間(t)（→日数として解釈）に対してプロットした結果は以下のようになります。
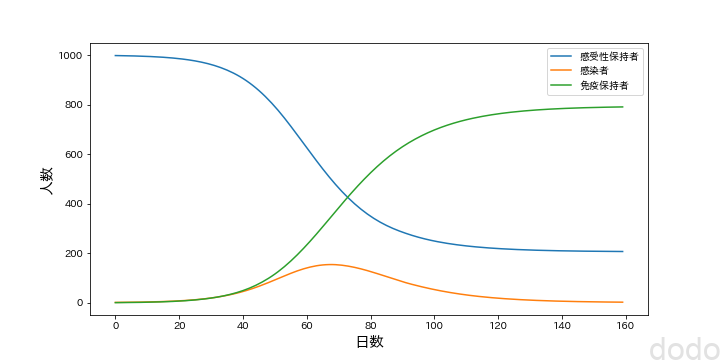SIRモデル（サンプル）徐々に感染者が増えていきますが、免疫保持者が増えるに連れて感染者が減っていく様子が示されています。
SIRモデルの実装（新型コロナの場合）
次に新型コロナと日本の感染状況をイメージした場合のSIRモデルを表現してみます。（間違ってもシミュレーションとか言いません・・）
\(\mathcal{R_{0}}\)はクラスター対策班が使用している2.5とします。
（この「2.5」という数字も日本の現状に即していないとの批判もあるようです。確かにこれ決め打ちするもんじゃない気もします・・）
回復率（\(\gamma\)）を求めれば、自動で感染率（\(\beta\)）も決まりますが、時間の単位を日付と考えた時、回復率（\(\gamma\)）の逆数が平均感染期間となるので、大雑把に２週間（１４日）と考えて、（\(\gamma=\frac{1}{14}\)）とします。
感受性保持者の初期値はこれも大雑把に日本の人口の1億2,600万人として、感染者の初期値は1人とします。
ソースコードは以下のようになります。
#トレース時間(1年)
T = 365
#人口≒感受性保持者初期値
S_0=126000000
#感染者初期値
I_0=1
#免疫保持者初期値
R_0=0
#基本再生産数
R0 = 2.5
#回復率(平均14日で回復)
gamma = 1 / 14
#感染率
beta = R0 * gamma / S_0
result = solve_ivp(SIR_wrapper(beta, gamma), [0, T], [S_0, I_0, R_0], t_eval=np.arange(0, T))
#plot
fig = plt.figure(figsize=(10, 5))
plt.title(f"R0={2.5}", fontsize=16)
plt.xlabel("日数",fontsize=15)
plt.ylabel("人数",fontsize=15)
plt.plot(result.t,result.y.T)
plt.legend(['感受性保持者','感染者', '免疫保持者'])
plt.savefig("./SIR_sample_japan.png")
plt.show()
以下、実行結果です。
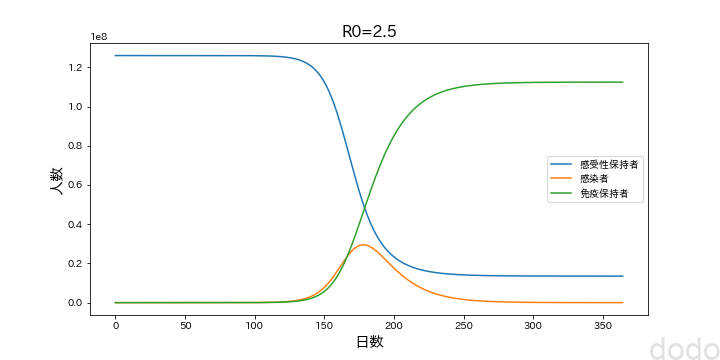SIRモデルサンプル（日本の感染状況をイメージ）このモデルだと、最初の感染から半年くらいがピーク（3,000万人！）で、１億1,000万人が最終的に免疫を取得（もしくは死亡・・）するような感じです。。
１月末に感染者が出たとすると夏までピークが続くような感じでしょうか・・（あくまでもモデル上の話です）
SIRモデルの実装（新型コロナ、接触減を考慮）
次に無謀にもクラスター対策班のモデルを再現する試みをしてみます。
ある時点で接触減の対策を実施した時、その時点で\(\mathcal{R_{t}}\)を調整します。（( 1-接触減率）をかけます。）
この接触減を0%(対策なし）、50%、60%、70%、80%とした場合のSIRモデルのグラフを描画します。
なお対策を実施した日付は初感染から90日目とします。
１月末初感染で４月末でようやくくらいなので、だいたいそんくらいかと・・（もっと前からやってたような気もしますが）
ソースコードは、以下となります。
#トレース時間(1年)
T = 365
#人口≒感受性保持者初期値
S_0_ini=126000000
#感染者初期値
I_0_ini=1
#免疫保持者初期値
R_0_ini=0
#90日前後で期間を分ける
periods = [[0,90],[90,T]]
#回復率(平均14日で回復)
gamma = 1 / 14
#基本再生産数
R0 = 2.5
fig = plt.figure(figsize=(15, 30))
fig.subplots_adjust(wspace=0.2, hspace=0.3)
for i,rate in enumerate([0.0,0.5,0.6,0.7,0.8]):
#90日経過前の初期値
S_0=S_0_ini
I_0=I_0_ini
R_0=R_0_ini
#基本再生産数
R0s = [R0, R0 * (1 - rate)]
#plot設定
ax1 = fig.add_subplot(5,2,2 * i + 1)
ax2 = fig.add_subplot(5,2,2 * i + 2)
for k,ax in enumerate([ax1,ax2]):
ax.set_xlabel("日数",fontsize=15)
ax.set_ylabel("人数",fontsize=15)
if k == 1:
ax.set_yscale("log")
ax.set_ylim(1,100000000)
else:
ax.set_ylim(0,20000)
for j,period in enumerate(periods):
#感染率
beta = R0s[j] * gamma / S_0
result = solve_ivp(SIR_wrapper(beta, gamma), period, [S_0, I_0, R_0], t_eval=np.arange(period[0], period[1]))
#90日経過後の初期値
S_0 = result.y[0][-1]
I_0 = result.y[1][-1]
R_0 = result.y[2][-1]
#plot
title = f"SIRモデル R0={2.5}, 接触削減率={rate:.1f}"
for k,ax in enumerate([ax1,ax2]):
ax.plot(result.t,result.y[1],color="orange")
ax.plot(result.t,result.y[2],color="green")
ax.legend(['感染者', '免疫保持者'],fontsize=15)
if k == 1:
ax.set_title(f"{title} (対数スケール)",fontsize=15)
else:
ax.set_title(f"{title} (線形スケール)",fontsize=15)
plt.savefig(f"./SIR_sample_japan_contact_reduce.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
以下、実行結果です。
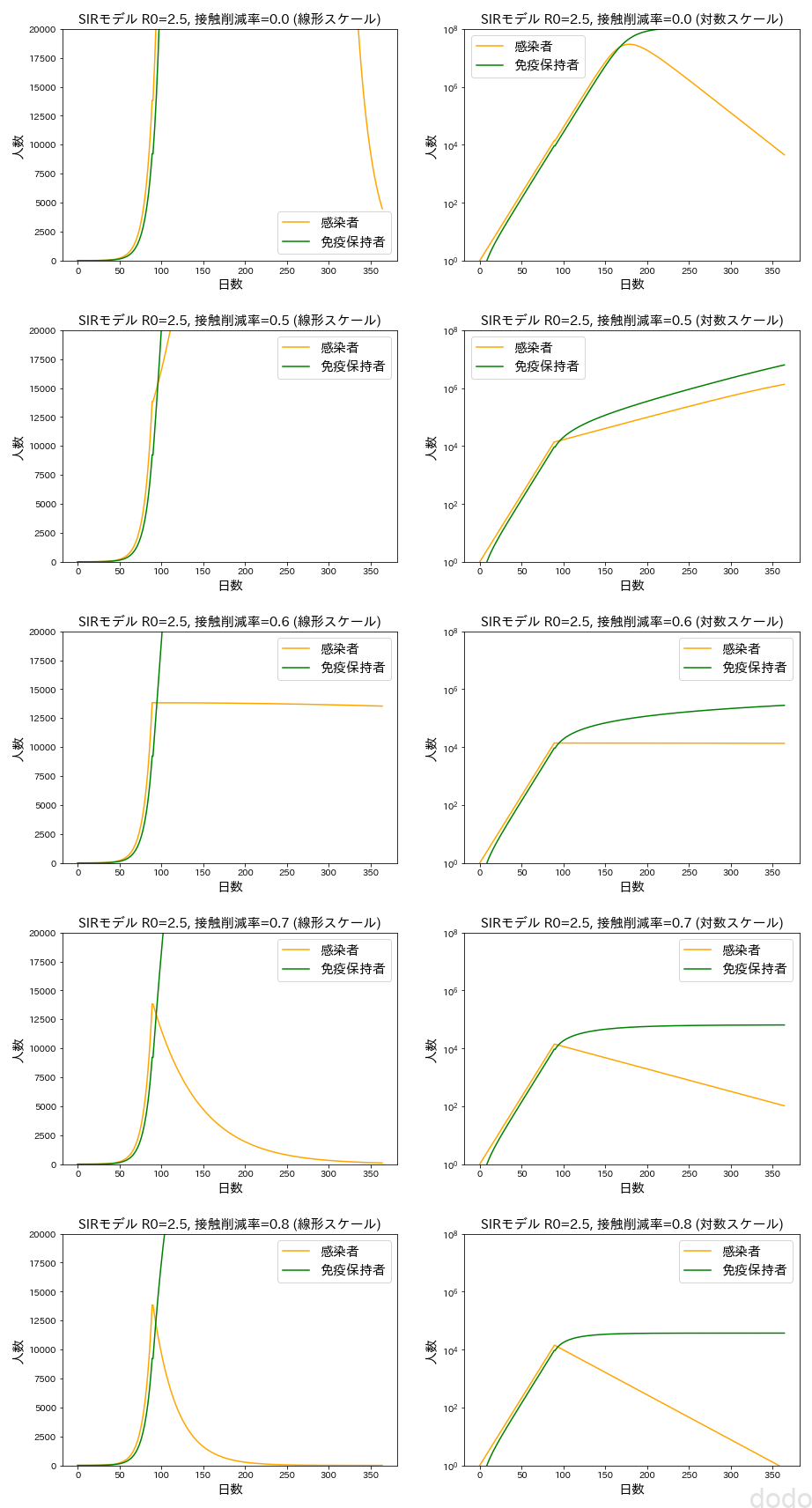SIRモデル（日本で接触率を減らした場合のイメージ）接触減を0%(対策なし）、50%、60%、70%、80%とした場合でそれぞれ線形スケール（左）と対数スケール（右）のグラフを描画してみました。
なお、\(S\)（感受性保持者）はスケールが違いすぎるので描画していません。
このグラフを見ると接触減が50%だと感染者が増加し（数千万人レベル！？）、60%だと感染者が横ばいで、それ以上だと感染者が減って行くように見えます。
こんな実データに全然フィッティングしていないような単純なモデルでも専門家が示したグラフと同じような振る舞いを示す事ができました。（数字は異なりますが・・）
因みに60%接触減を境いに感染者数が上昇/下降するのは、60%の場合、基本再生産数が\(2.5\times (1 – 0.6) = 1\)、つまり1人が1人に感染させる事になるので、当たり前といえば当たり前です。
SIR-Fモデル
やっぱり、死者数がどれくらい出るかって重要ですよね。。
SIRモデルだと\(R\)（免疫保持者）に死者数も混じってしまっているので、そこらへんがよくわかりません。（治るのと死ぬのとでは大違いです。）
調べて見ると、SIR-Fモデルという死者数を考慮に入れるモデルもあるようで、そちらも試してみることにしました。
SIR-Fモデルは\(S\)（感受性保持者）、\(I\)（感染者）、\(R\)（免疫保持者）に加えて\(F\)（死者）が追加され、以下のような微分方程式で表現できます。
\begin{eqnarray}
\frac{dS(t)}{dt} &=&-\beta S(t) I(t)\\
\frac{dI(t)}{dt} &=&\beta (1-\alpha_1) S(t) I(t) – (\gamma + \alpha_2) I(t)\\
\frac{dR(t)}{dt} &=&\gamma I(t)\\
\frac{dF(t)}{dt} &=&\beta \alpha_1 S(t) I(t) + \alpha_2 I(t)\\
\end{eqnarray}
ここで新たに登場する\(\alpha_1\)は感染者と判定される前の致死率、\(\alpha_2\)は感染者と判定されてからの致死率となります。
フローで表すと以下のようになります。
\begin{eqnarray}
\Large S&\Large\,\overset{\beta I}{\rightarrow}\,&\Large S^{*}&\Large\,\overset{\alpha_1}{\rightarrow}\,&\Large F\\
&&\Large &\Large\,\overset{1-\alpha_1}{\rightarrow}\,&\Large I&\Large\,\overset{\gamma}{\rightarrow}\,&\Large R\\
&&&&&\Large \,\overset{\alpha_2}{\rightarrow}\,&\Large F\\
\end{eqnarray}
基本再生産数は以下のようになります。
$$\mathcal{R_{0}} = \frac{\beta (1- \alpha_1) S_{0}}{\gamma+\alpha_2} $$
SIR-Fモデルの実装（新型コロナ、接触減を考慮）
SIR-FモデルでもSIRモデルと同様に接触を減らしていった場合の感染者数などの状況を可視化してみましょう。
SIR-Fモデルは以下のような関数となります。（SIRモデルと同様にsolve_ivp用に関数内関数として定義しています。）
def SIRF_wrapper(beta, gamma, alpha1, alpha2):
def SIRF(t, y):
dSdt = -beta * y[0] * y[1]
dIdt = beta * (1 - alpha1) * y[0] * y[1] - (gamma + alpha2) * y[1]
dRdt = gamma * y[1]
dFdt = beta * alpha1 * y[0] * y[1] + alpha2 * y[1]
return [dSdt, dIdt, dRdt, dFdt]
return SIRF
SIRモデルの可視化のソースをSIR-Fモデル用に修正します。
#トレース時間(1年)
T = 365
#人口≒感受性保持者初期値
S_0_ini=126000000
#感染者初期値
I_0_ini=1
#免疫保持者初期値
R_0_ini=0
#死者初期値
F_0_ini=0
#90日前後で期間を分ける
periods = [[0,90],[90,T]]
#回復率(平均14日で回復)
gamma = 1 / 14
#判定前死亡率（わからないので０）
alpha1 = 0
#死亡率(だいた2%の人が亡くなると想定)
alpha2 = gamma * 0.02 / (1 - 0.02)
#基本再生産数
R0 = 2.5
fig = plt.figure(figsize=(15, 30))
fig.subplots_adjust(wspace=0.2, hspace=0.3)
for i,rate in enumerate([0.0,0.5,0.6,0.7,0.8]):
#90日経過前の初期値
S_0=S_0_ini
I_0=I_0_ini
R_0=R_0_ini
F_0=F_0_ini
#基本再生産数
R0s = [R0, R0 * (1 - rate)]
#plot設定
ax1 = fig.add_subplot(5,2,2 * i + 1)
ax2 = fig.add_subplot(5,2,2 * i + 2)
for k,ax in enumerate([ax1,ax2]):
ax.set_xlabel("日数",fontsize=15)
ax.set_ylabel("人数",fontsize=15)
if k == 1:
ax.set_yscale("log")
ax.set_ylim(1,100000000)
else:
ax.set_ylim(0,20000)
for j,period in enumerate(periods):
#感染率
beta = R0s[j] * (gamma + alpha2) / (1 - alpha1) / S_0
result = solve_ivp(SIRF_wrapper(beta, gamma, alpha1, alpha2), period, [S_0, I_0, R_0, F_0], t_eval=np.arange(period[0], period[1]))
#90日経過後の初期値
S_0 = result.y[0][-1]
I_0 = result.y[1][-1]
R_0 = result.y[2][-1]
F_0 = result.y[3][-1]
#plot
title = f"SIR-Fモデル R0={2.5}, 接触削減率={rate:.1f}"
for k,ax in enumerate([ax1,ax2]):
ax.plot(result.t,result.y[1],color="orange")
ax.plot(result.t,result.y[2],color="green")
ax.plot(result.t,result.y[3],color="red")
ax.legend(['感染者', '免疫保持者', '死者'],fontsize=15)
if k == 1:
ax.set_title(f"{title} (対数スケール)",fontsize=15)
else:
ax.set_title(f"{title} (線形スケール)",fontsize=15)
plt.savefig(f"./SIRF_sample_japan_contact_reduce.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
判定前の致死率(\(\alpha_1\))は、よくわからないので0にしました。
判定後の致死率(\(\alpha_2\))については、これも諸説ありますが2%といった記載をよく見かけるので、免疫保持者となる人数と死亡する人数が98:2の割合だとして算出しました。
以下、実行結果です。
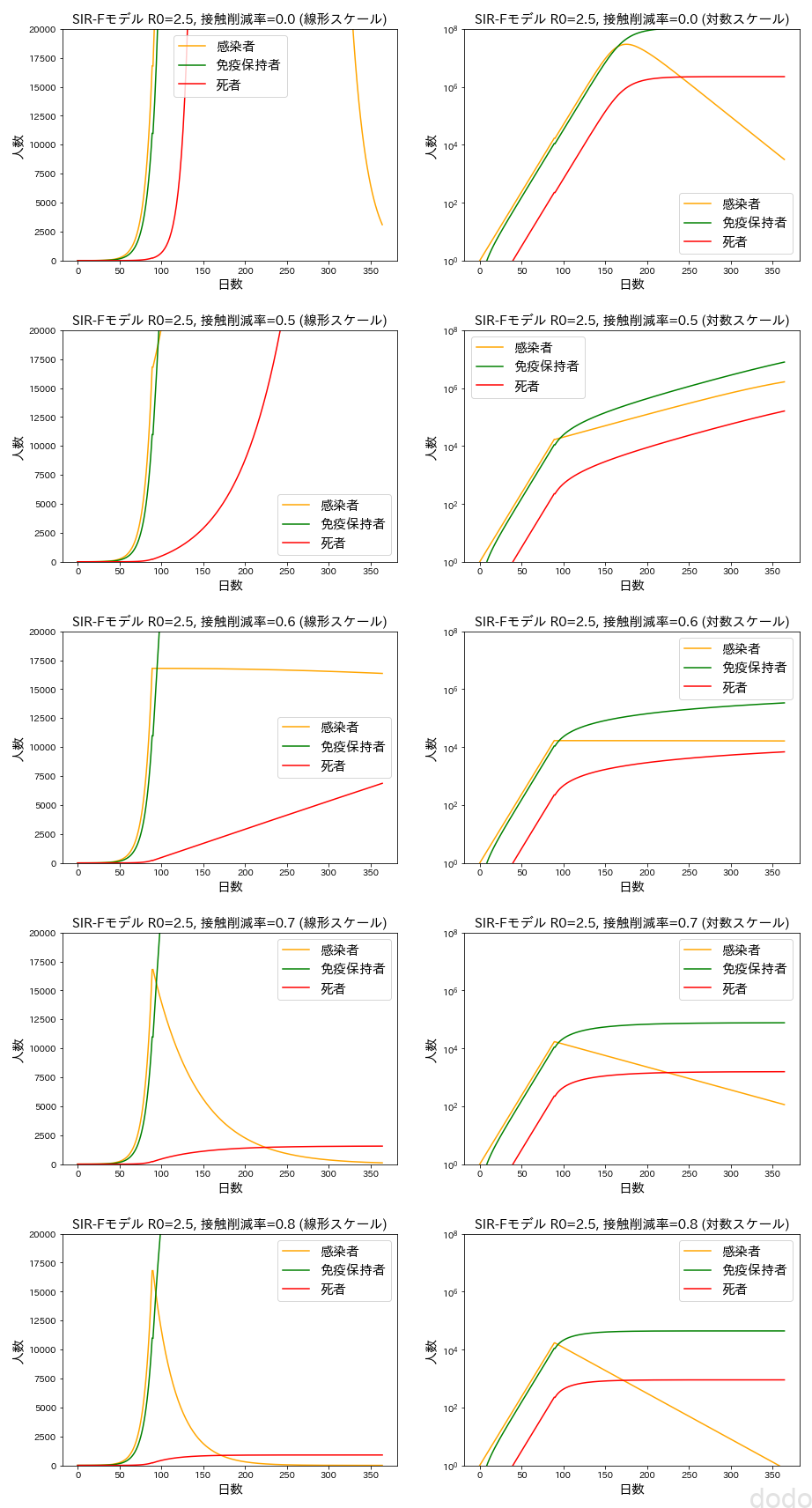SIR-Fモデル（日本で接触率を減らした場合のイメージ）６割の接触減だと死者数が増加していきますが、７割以上だと落ち着く感じですね。
いわゆる何も対策しない場合は、このなんちゃってモデルだと100万人死んじゃいます（！）が、8割の接触削減だと1000人程度に収まります。
まとめ
以上、SIRモデルとSIR-FモデルをPythonで実装した結果について記載しました。
この程度の簡単な数理モデルならばライブラリの力は借りましたが、割と簡単に実装できるものです。
繰り返しますが、この記事は現在流行している新型コロナの感染状況を真面目に分析したものではありません。
こんなの、ぶっちゃけパラメータ次第でどうにでも結果を変えられます。
真面目にやるならば、潜伏期間、検査待ち数、検査数、ベッドの数、人工呼吸器の数なども考慮して、パラメータも最新のデータにフィッティングして、決定する必要があります。
きっと世界中の研究者が血眼になってやっている事でしょう。
ただ個人的には、そのような事を念入りにやったとしても、新種のウィルスの動向を予測するのはかなり難しいと思います。。
