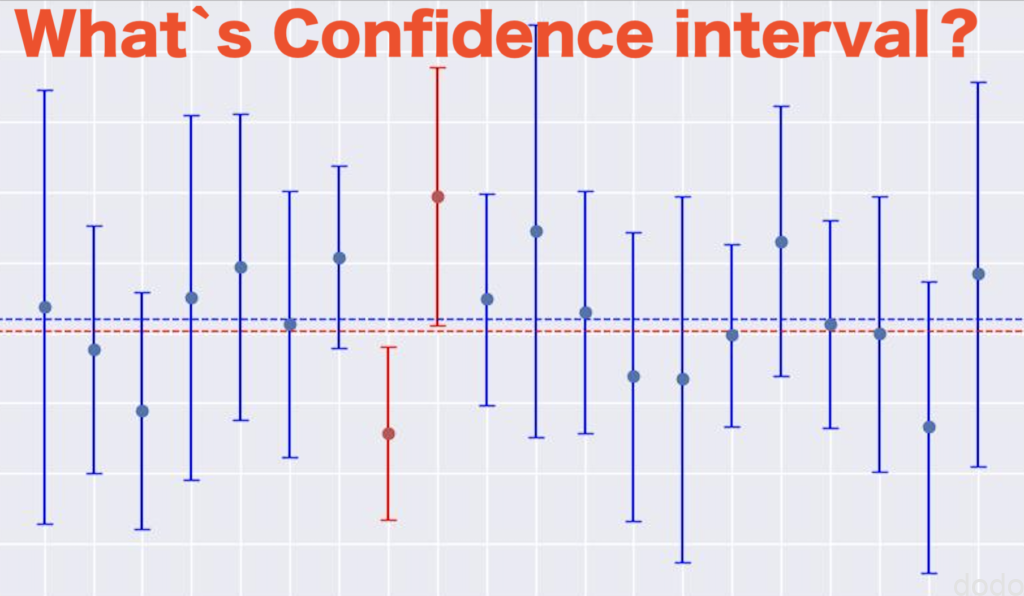
統計で信頼区間と言えば、誤った解釈をされがちなものとして有名です。
標本の平均の95%の信頼区間を求めた場合、母集団の平均がその区間内に収まる確率が95%ではありません。
1つの標本で95%の確率でその区間内に入っているという解釈は間違っています。
95%の信頼区間は、母集団から複数回、標本を抽出した時に100回中(だいたい)95回が信頼区間内に母集団が入っている割合として解釈されます。
この件は言葉だけではなかなか理解しにくいので、本記事では実際に可視化して確かめてみます。
本記事のグラフ内で「標本数」と記載されているものは、正しくは「標本サイズ」ですので読み替えてください。(後日、修正します。)
信頼区間の可視化
前提条件
本ソースコードは、Python3.7.5で起動するJupyter Lab上で実行されています。
また使用している各ライブラリのバージョンは以下の通りです。
- numpy(1.20.3)
- scipy(1.5,4)
- matplotlib(3.5.1)
- seabon(0.11.2)
可視化の準備
今回は可視化のためにmatplotlib+seabonを使用します。
文字フォント、文字の大きさなどについて以下のように設定します。
import matplotlib.pyplot as plt
import seaborn as sns
#図形のサイズ
plt.rcParams["figure.figsize"] = (10, 6)
#フォントの大きさ
plt.rcParams["font.size"] = 15
#使用フォント
sns.set(font='Hiragino Sans')母集団の生成
まずは母集団を生成します。
母集団は、\(X \sim N(10,3^2)\) (平均10、標準偏差3の正規分布)に従う10000件のデータとします。
import numpy as np
parent_set_normal = np.random.normal(loc=10.0, scale=3.0, size=10000)
ヒストグラムを出力して画像を保存します。
def plot_hist(data, file_name, bins=20):
"""
ヒストグラムを生成して保存する。
Parameters
----------
data : ndarray
ヒストグラムを表示するデータのndarray
file_name : string
保存ファイル名
bins : int , default 20
階級
"""
plt.hist(data,bins)
plt.tight_layout()
plt.savefig(file_name, dpi=100)plot_hist(parent_set_normal,'parent_set_normal_hist_10_3.jpg')
実行すると以下のようなヒストグラムが出力されます。
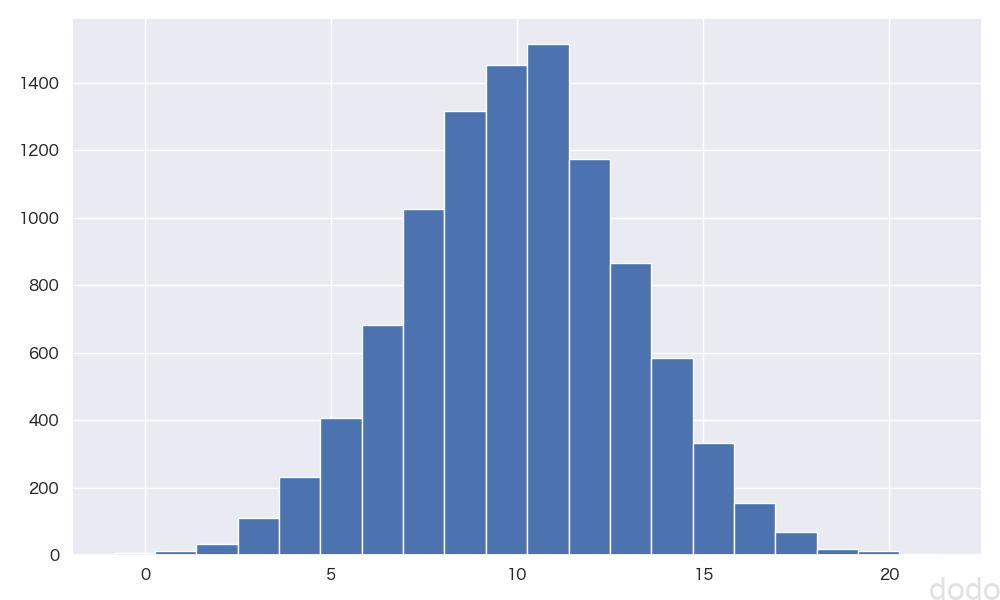 正規分布N(10,9)のヒストグラム
正規分布N(10,9)のヒストグラム
標本の抽出
生成した母集団から標本を抽出します。
試しに10件だけ抽出してみましょう。
import random
def get_sample(parent_set,sample_size):
"""
標本を取得する。
Parameters
----------
parent_set : ndarray
母集団のデータ
sample_size : int
標本サイズ
Returns
-------
sample : ndarray
標本データ
"""
indexes = random.sample(range(parent_set.size), k=sample_size)
return parent_set[indexes]sample = get_sample(parent_set_normal,10)
抽出した標本の平均は以下の値となります。
print(sample.mean())実行結果:10.032263045696737
たった10件ですが、母集団平均に近い値になっています。
次に標本の平均の95%信頼区間を調べてみましょう。
ここでは母集団の分散は未知として扱うので、t分布を利用した区間推定の手法を用います。
from scipy import stats
def get_interval(sample, alpha):
"""
標本の信頼区間を返す。
Parameters
----------
sample : ndarray
標本データ
alpha : int
信頼水準
Returns
-------
interval : (float,float)
信頼区間(下限、上限)
"""
#母集団の分散は未知として、t分布から信頼区間を求める。
t_dist = stats.t(loc=sample.mean(),
scale=np.sqrt(sample.var()/sample.size),
df=sample.size-1)
return t_dist.interval(alpha=alpha)
抽出した標本平均の95%信頼区間の下限、上限は以下となります。
print(get_interval(sample, 0.95))実行結果: (7.649149811635002, 12.415376279758473)
複数の標本の信頼区間を可視化
冒頭で記載したとおり、算出した95%信頼区間は、母集団の平均がこの区間内にある確率が95%という事を意味しておりません。
この95%という数字は、複数回、標本を算出した時に母集団が区間内に含まれる割合です。
この事を理解するために標本を複数回、抽出して確かめてみましょう。
以下のような関数を作成して、標本を複数回、抽出して可視化します。(詳細な説明は省略します。ソース内のコメントをご参照ください。)
def interval_test(parent_set, sample_size, sampling_count, alpha):
"""
与えられた試行回数分、標本を抽出して信頼区間を可視化する。
Parameters
----------
parent_set : ndarray
母集団データ
sample_size : int
標本サイズ
sampling_count : int
試行サイズ
alpha : float
信頼水準
Returns
-------
mean,interval : (ndarray,ndarray,ndarray)
各標本の平均と信頼区間(下限、上限)のNumpy配列
"""
#figure
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
#母集団平均が信頼区間内に入った回数
interval_in_cnt = 0
#母集団平均
parent_mean = parent_set.mean()
#標本の平均、信頼区間下限、上限
means = []
bottoms =[]
tops = []
#サンプリング回数分繰り返す
for i in range(sampling_count):
#標本取得
sample = get_sample(parent_set, sample_size)
#標本平均
sample_mean = sample.mean()
means.append(sample_mean)
#信頼区間取得
bottom, top = get_interval(sample, alpha)
bottoms.append(bottom)
tops.append(top)
#母集団平均が信頼区間内かどうか
interval_in = parent_mean >= bottom and parent_mean<=top
#母集団平均が信頼区間内に入った回数(信頼区間カウント)
interval_in_cnt += 1 if interval_in else 0
#信頼区間内の場合は青、信頼区間外の場合は赤とする
fmt, ecolor = ('bo', 'blue') if interval_in else ('ro', 'red')
#信頼区間内、区間外の凡例設定(それぞれ一回のみ表示)
if interval_in_cnt == 1 and interval_in:
#初めて信頼区間内の場合(信頼区間カウントが1で信頼区間内)
label = '母集団平均が区間内'
elif interval_in_cnt == i and not interval_in:
#初めて信頼区間外の場合(信頼区間カウント=標本回数-1で信頼区間外)
label = '母集団平均が区間外'
else:
label = ''
#信頼区間をエラーバーとして表示
ax.errorbar(i+1, sample_mean, [[sample_mean-bottom],[top-sample_mean]], fmt=fmt, capsize=4, label=label, ecolor=ecolor)
#母集団平均をlineで表示
ax.hlines(parent_mean,0,sampling_count+1, color='red', ls='dashed',lw=1, label=f'{parent_mean:.2f}(母集団平均)')
#標本平均の平均をlineで表示
means_means = sum(means)/len(means)
ax.hlines(means_means,0,sampling_count+1, color='blue', ls='dashed',lw=1, label=f'{means_means:.2f}(標本平均の平均)')
#描画範囲
ax.set_xlim([0, sampling_count+1])
ax.xaxis.set_ticks(np.arange(1, sampling_count+1, 1))
#タイトル、ラベル設定
ax.set_xlabel(f'試行回数 (信頼区間に入った標本は{interval_in_cnt/sampling_count:.1%})')
ax.set_title(f'{alpha:.0%}信頼区間 (標本サイズ:{sample_size}、試行回数:{sampling_count})')
ax.legend(bbox_to_anchor=(1.02, 1), loc='upper left')
plt.savefig(f'sampling_test_{sample_size}_{sampling_count}_{alpha}.jpg', dpi=100, bbox_inches='tight')
return np.array(means),np.array(bottoms),np.array(tops)
標本サイズ10、試行回数20での95%信頼区間を表示します。
_ = interval_test(parent_set_normal, 10, 20, 0.95)
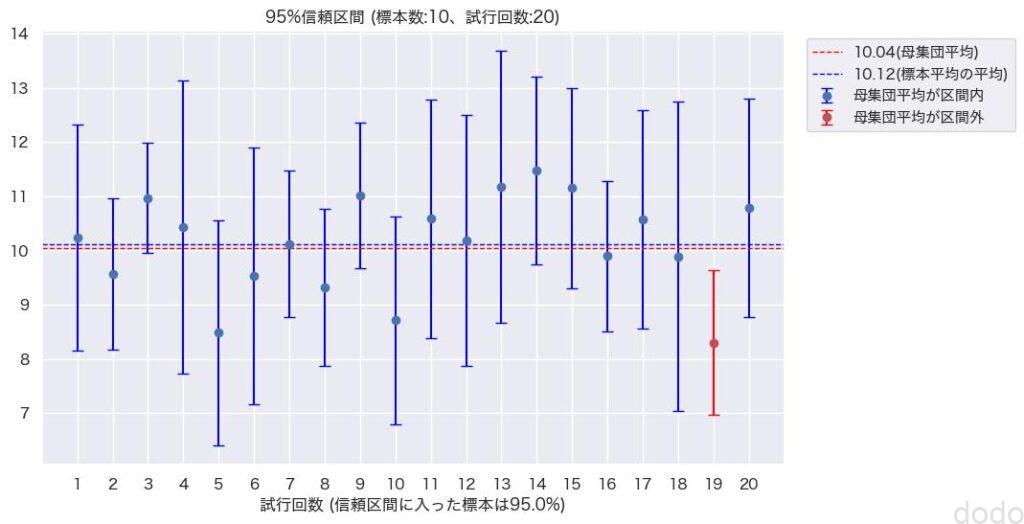
上記を実行すると、以下のグラフが出力されます。
 95%信頼区間(標本サイズ10,試行回数20)
95%信頼区間(標本サイズ10,試行回数20)横軸が試行回数、縦軸が母集団平均、試行して抽出した標本に対する標本平均と信頼区間のデータとなっております。
結果を見ると、20回、標本を抽出した結果、20回中19回が信頼区間の中に母集団平均を含んでいる事になります。
この20回中19回の割合が信頼水準の95%に対応する数字となります。
もちろん、ランダム抽出なので、常に結果が95%に一致する訳ではありません。
95%信頼区間を求めていても、何度も実行すれば以下のように100%の結果になったり、90%の結果になったりします。
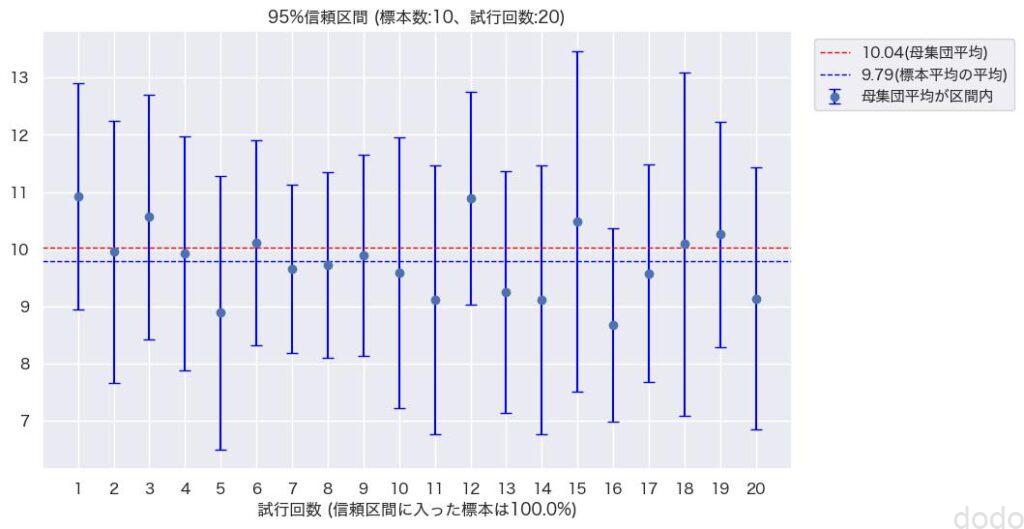 95%信頼区間(標本サイズ10,試行回数20) 結果100%信頼区間内になった場合
95%信頼区間(標本サイズ10,試行回数20) 結果100%信頼区間内になった場合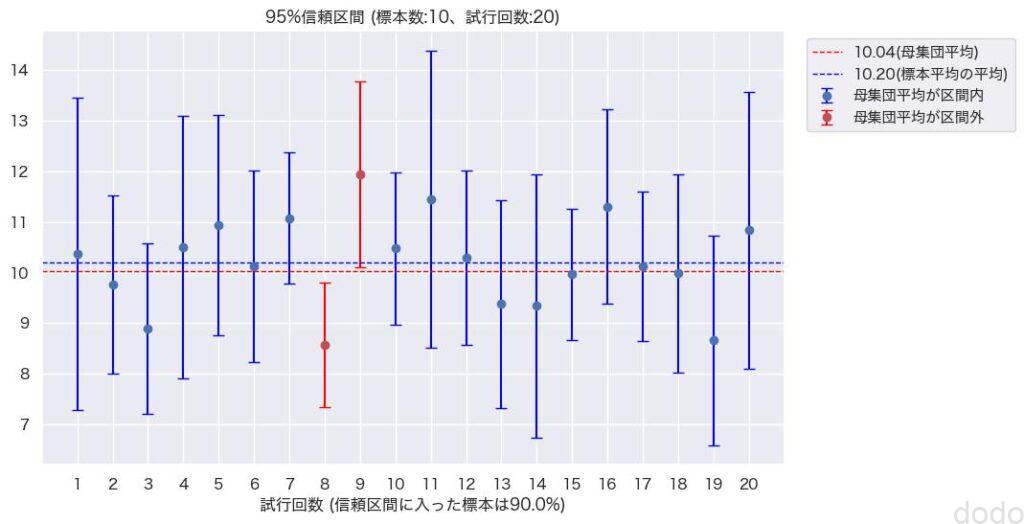 95%信頼区間(標本サイズ10,試行回数20) 結果90%信頼区間内になった場合
95%信頼区間(標本サイズ10,試行回数20) 結果90%信頼区間内になった場合ただ、いずれにせよだいたい95%の標本の信頼区間に母集団平均が含まれるのがわかります。
そして、1つの標本の信頼区間を見て、その区間内に母集団平均が含まれる確率が95%という表現が間違っているのもわかると思います。(この表現だと標本平均に近づくほど、確率が高いようなイメージを持ってしまいそうですが、図を見ればそうではない事がわかると思います。)
まとめ
以上、信頼区間の意味合いについて実際に可視化して確かめてみました。
あくまでも95%信頼区間の「95%」は、複数回、標本を抽出した場合の割合の数字です。
確率と割合の違いの意味はなかなか混同しがちですが、このように可視化すると少しわかりやすくなるかと思います。
なお、上記のコードで信頼水準95%を他の数字に変更すると、だいたいその変更した数字の近辺の割合の結果が出ますし、サンプル数を大きくすると信頼区間の幅が狭くなったりしますので、余裕がある方は試してみてください。