統計学の有名な定理として、中心極限定理というものがあります。
標本（サンプルサイズ\(n\)）を母集団（平均\( \mu\)、分散\(\sigma^2\)）から抽出したとき、\(n\)が大きくなるほど、標本平均の分布は、平均\( \mu\)、分散\(\sigma^2/n\)の正規分布（\(X \sim N(\mu ,\sigma^2/n)\) ）に近づくという定理です。
ポイントは、母集団の分布は、期待値と分散が求められるような母集団ならばどのような分布であってもよい事です。
本記事では、実際に母集団から標本を抽出して、中心極限定理に従うのかを実際に可視化して検証してみます。
中心極限定理の検証
前提条件
本ソースコードは、Python3.7.5で起動するJupyter Lab上で実行されています。
また使用している各ライブラリのバージョンは以下の通りです。
- numpy(1.20.3)
- scipy(1.5,4)
- matplotlib(3.5.1)
- seaborn(0.11.2)
可視化の準備
今回は可視化のためにmatplotlib+seabonを使用します。
文字フォント、文字の大きさなどについて以下のように設定します。
import matplotlib.pyplot as plt
import seaborn as sns
#図形のサイズ
plt.rcParams["figure.figsize"] = (10, 6)
#フォントの大きさ
plt.rcParams["font.size"] = 15
#使用フォント
sns.set(font='Hiragino Sans')母集団の生成
まずは母集団を生成します。
母集団は、\(X \sim N(10,3^2)\) （平均10、標準偏差3の正規分布）に従う1万件のデータとします。
信頼区間を可視化する前回の記事では、np.random.normalを使用しましたが、今回は、scipy.stats.normを使用して生成します。（scipy.stats.normでnp.random.normalを呼び出しているので結局は同じ機能が使用されますが、今回はscipy.statsを利用した方が後のクラス化などで都合が良いので、こちらを使用します。）
from scipy import stats
parent_set_normal = stats.norm.rvs(loc=10, scale=3, size=10000)
ヒストグラムを出力して画像を保存します。（今回は形状だけ見たいので相対度数で表示します。(density=True)）
def plot_hist(data, file_name, bins=20):
"""
ヒストグラムを生成して保存する。(相対度数)
Parameters
----------
data : ndarray
ヒストグラムを表示するデータのndarray
file_name : string
保存ファイル名
bins : int , default 20
階級
"""
plt.hist(data, bins, density=True)
plt.tight_layout()
plt.savefig(file_name, dpi=100)plot_hist(parent_set_normal, 'parent_set_normal.jpg')
実行すると以下のようなヒストグラムが出力されます。
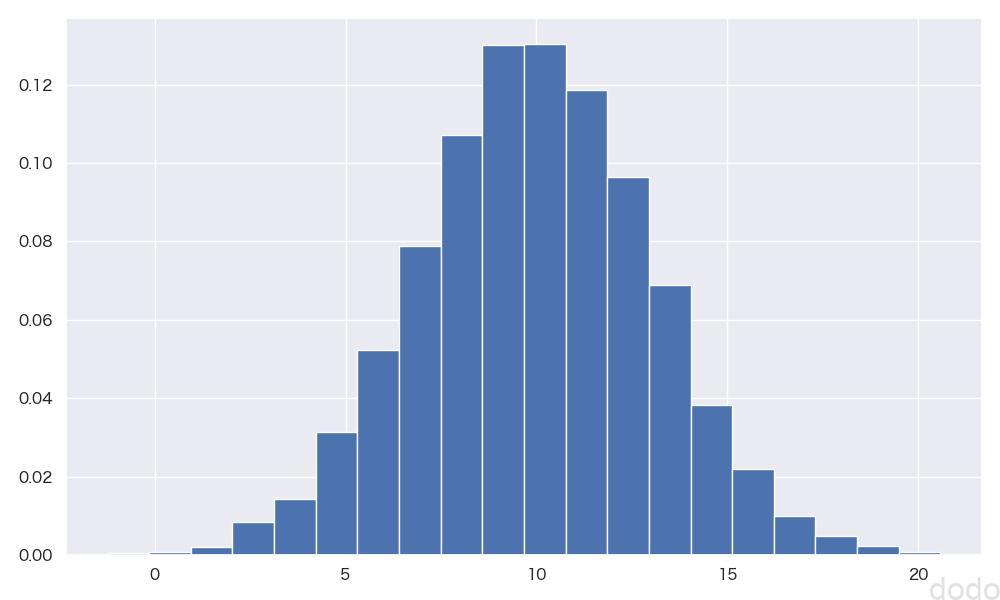正規分布（\(X \sim N(10,3^2)\) ）ヒストグラムdistributionクラスの作成
今回、確率密度関数とデータのヒストグラムを描写して比較することを繰り返しますが、汎用性を持たせるためにクラスを作成します。
クラスのコードは以下となります。
import numpy as np
class distribution:
"""
scipy.statsの分布の乱数データ、確率密度分布を生成し、それらを可視化する。
Methods
-------
rvs
pdf
plot_hist
"""
def __init__(self, dist, rvs_size=10000, pdf_x_size=100, **sts_kwds):
"""
初期化
与えられた分布情報から乱数（rvs）,確率密度分布(pdf)を生成する。
Parameters
----------
dist : callable
scipy.statsに所属する分布
rvs_size : int, default 1000
生成する乱数の数
pdf_x_size : int, default 100
確率密度分布のため生成するX軸の点の数
sts_kwds : dictionary
分布生成のための引数(loc,scaleなど）
"""
self.__rvs = dist.rvs(size=rvs_size, **sts_kwds)
self.__x = np.linspace(dist.ppf(0.005,**sts_kwds),
dist.ppf(0.995,**sts_kwds),
pdf_x_size)
self.__pdf = dist.pdf(self.__x, **sts_kwds)
def rvs(self):
"""
分布の乱数を返す。
Return
----------
rvs : ndarray
生成した乱数
"""
return self.__rvs
def pdf(self):
"""
確率密度分布を生成して返す。
Return
----------
pdf : ndarray
生成した確率密度分布の値
"""
return self.__pdf
def plot_hist(self, ax=None, data=[], file_name="",
is_plot_rvs=True, is_plot_pdf=True, **plt_kwds):
"""
ヒストグラム(相対頻度）と確率密度分布を描画する。
描画するデータは最大３データ。
data 外部データ、分布に従って生成されたランダムデータと確率密度関数
Parameters
----------
ax : axes, default None
描画するaxes Noneの場合は内部で生成
data : array_like, default []
ヒストグラムを表示する外部データ
file_name : string, default ""
保存ファイル名 (""の場合は保存しない）
is_plot_rvs : bool, defalut True
rvsを描写するかどうかのフラグ
is_plot_pdf : bool, defalut True
pdfを描写するかどうかのフラグ
plt_kwds : dictionary
axes#histに渡す引数
"""
if ax is None:
fig, ax = plt.subplots()
if is_plot_rvs:
ax.hist(self.__rvs, density=True, color='b', **plt_kwds, label="rvs")
if is_plot_pdf:
ax.plot(self.__x, self.__pdf, color='r', label="pdf")
if len(data) != 0:
ax.hist(data, density=True, color='g', **plt_kwds, label="data")
ax.legend(loc='upper right')
if file_name != "":
plt.tight_layout()
plt.savefig(file_name, dpi=100)
本クラスは、scipy.statsが提供する様々な分布生成関数(rv_continuous継承クラスのインスタンス）をラッピングするクラスです。
分布生成関数や分布の情報などをもとにイン寸タンスを生成すると、内部で分布に基づく乱数(rvs)と確率密度関数(pdf)のデータを生成します。
plot_histメソッドによって、乱数データのヒストグラムと確率密度関数を可視化することができます。
以下のコードは、正規分布（\(X \sim N(10,3^2)\) ）を生成して可視化します。
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':20, 'alpha':0.8}
#正規分布を生成
norm = distribution(stats.norm,**sts_kwds)
#正規分布を可視化
norm.plot_hist(**plt_kwds, file_name="norm_distribute.jpg")実行すると以下のような結果になります。
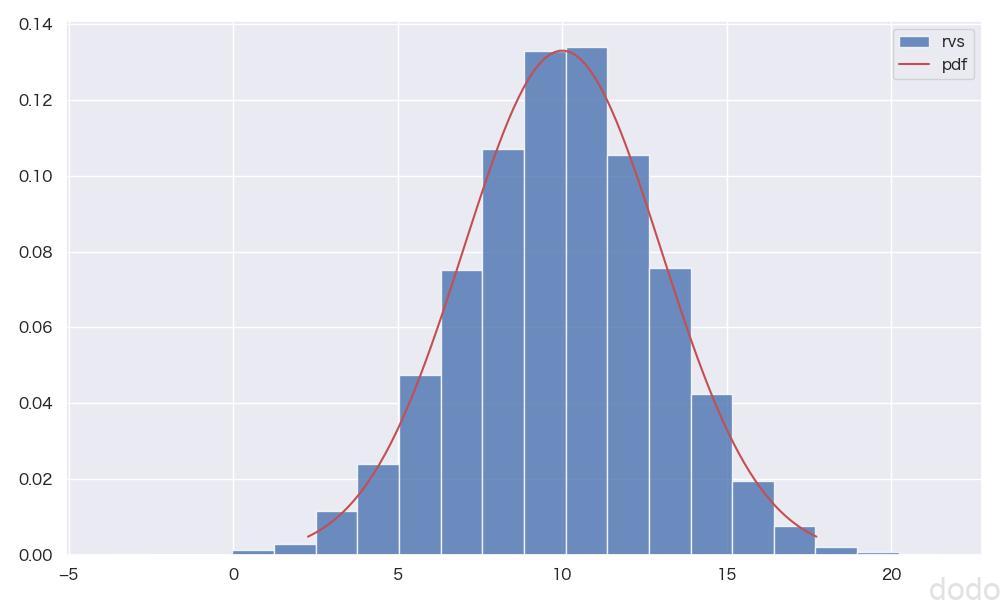正規分布（\(X \sim N(10,3^2)\) ）（ヒストグラムと確率密度関数の比較）また、以下のように外部から別のデータ（正規分布データ（\(X \sim N(13,5^2)\) ）を渡して、そのデータのヒストグラムを一緒に表示することもできます。
norm.plot_hist(
data=stats.norm.rvs(loc=13, scale=5, size=10000),
file_name="norm_distribute_with_data.jpg",
**plt_kwds
)実行すると以下のような結果になります。
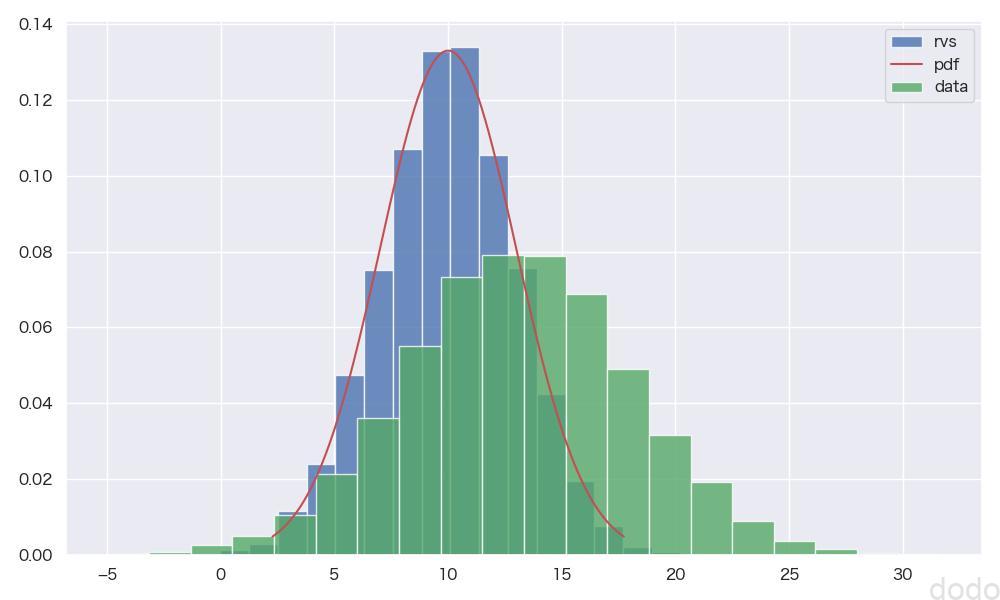正規分布の比較標本平均の分布の可視化
母集団から標本を抽出して、標本平均のヒストグラムと正規分布（\(X \sim N(\mu ,\sigma^2/n)\) ）の確率密度関数を比較して表示します。(\( \mu\)は母集団の平均、\(\sigma^2\)は母集団の分散、\(n\)はサンプルサイズ）
このために以下のような関数を作成します。
まずは標本抽出のための関数を作成します。（簡単なので説明は省略します。）
import random
def get_sample(parent_set,sample_size):
"""
標本を取得する。
Parameters
----------
parent_set : ndarray
母集団のデータ
sample_size : int
標本サイズ
Returns
-------
sample : ndarray
標本データ
"""
indexes = random.sample(range(parent_set.size), k=sample_size)
return parent_set[indexes]
次に、繰り返し標本を抽出してヒストグラムを表示する関数を作成します。
import math
def plot_sample_mean_distribution(sample_size_list, sampling_count,
parent_set, file_name="", bins=30, col=2):
"""
サンプルサイズごとに平均の分布を中心極限定理により従うべき分布と比較して表示する。
合わせてシャピロ・ウィルク検定とコルモゴロフ–スミルノフ検定の結果も表示する。
Parameters
----------
sample_size_list : arry_like
標本サイズの配列。それぞれについてグラフを表示する。
sampling_count : int
標本の取得回数
parent_set : ndarray
母集団データ
file_name : string ,default ""
保存ファイル名
bins : int ,default 30
ヒストグラムの階級
col : int ,default 2
グラフの列数
"""
#figureオブジェクト
fig = plt.figure(figsize=(20,20))
#グラフの行数
row = math.ceil(len(sample_size_list) / col)
'''
サンプルサイズの配列分、ヒストグラムを可視化する。
'''
for cnt,sample_size in enumerate(sample_size_list):
#標本平均の配列
means = []
'''
中心極限定理で比較するための分布
'''
#中心極限定理により従うべき分布の平均と標準偏差
mean = parent_set.mean()
scale = parent_set.std()/np.sqrt(sample_size)
sts_kwds ={'loc' : mean, 'scale' : scale}
'''
指定されたサンプル数ごとに標本の取得を繰り返して標本平均を取得
'''
for i in range(sampling_count):
#標本取得
sample = get_sample(parent_set, sample_size)
means.append(sample.mean())
#コルモゴロフ–スミルノフ検定 P値
pvalue_ks = stats.kstest(means,stats.norm(**sts_kwds).cdf).pvalue
#シャピロ・ウィルク検定 P値
pvalue_sw = stats.shapiro(means).pvalue
#axオブジェクト追加
ax = fig.add_subplot(row,col,cnt+1)
#タイトル設定（サンプル数、シャピロ・ウィルク検定 P値、コルモゴロフ–スミルノフ検定 P値）
ax.set_title(f'n={sample_size}'\
f' p-value(sw)={pvalue_sw:.2f}'\
f' p-value(ks)={pvalue_ks:.2f}',
fontsize=20)
#標本平均のヒストグラム描写
dist = distribution(stats.norm, **sts_kwds)
plt_kwds = {'bins':bins, 'alpha':0.8}
dist.plot_hist(ax=ax, data=means, is_plot_rvs=False,
is_plot_pdf=True, **plt_kwds)
if file_name != "":
plt.tight_layout()
plt.savefig(file_name, dpi=100)
引数にサンプルサイズの配列を指定して、サンプルサイズごとに、指定したカウント分の標本抽出を繰り返してグラフを表示します。
サンプルサイズごとのグラフには標本平均のヒストグラムと中心極限定理により従うべき確率密度関数を表示するとともに、正規分布に従っているかどうかの検定結果も表示します。
今回、使用する検定は以下の２つです。
- シャピロ・ウィルク検定（S-W検定）
- コルモゴロフ–スミルノフ検定（K-S検定）
詳細は省きますが、S-W検定ではデータが正規分布と異なるかどうか、K-S検定ではデータが別の確率分布と異なるかどうかを検定します。
上記で「同じかどうか」ではなく「異なるかどうか」と記載したのは意味があります。検定でP値が0.05以上だとしても「同じである」事を意味するのではなく「異なるとは言えない」という事だけです。（帰無仮説が棄却できないからと言って帰無仮説が正しいとは言えないということです。）
K-S検定にscipy.stats.kstestを使用していますが、最初インターフェースがよくわからずに中身のコードを見てようやく理解しました・・
引数に、rvs、cdfとありますが、両方に配列データを与えた場合は２つのデータの経験分布を比較し、rvsに配列データ、cdfに関数(callable)を与えた場合はrvsの経験分布とcdf(累積密度関数）を比較します。
※最初、cdfにcdfの関数ではなくデータを渡してしまったため前者（両方に配列データを与えた場合）と判定されて、全く間違った結果が出て悩みました・・
母集団が正規分布の場合
正規分布の母集団から抽出した標本の場合に中心極限定理を確かめてみましょう。
まずは母集団を生成します。
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':20, 'alpha':0.8}
#正規分布を生成
norm = distribution(stats.norm,**sts_kwds)
#正規分布を可視化
norm.plot_hist(**plt_kwds, file_name="norm_distribute.jpg")
#乱数データを取得
parent_set_norm = norm.rvs()この母集団をもとに標本のサンプルサイズ1,2,5,10,100,1000毎に1000回の抽出を繰り返してヒストグラムを可視化します。
plot_sample_mean_distribution([1,2,5,10,100,1000],
1000,
parent_set_normal,
file_name='norm_sample_mean.jpg')実行すると以下のような結果になります。
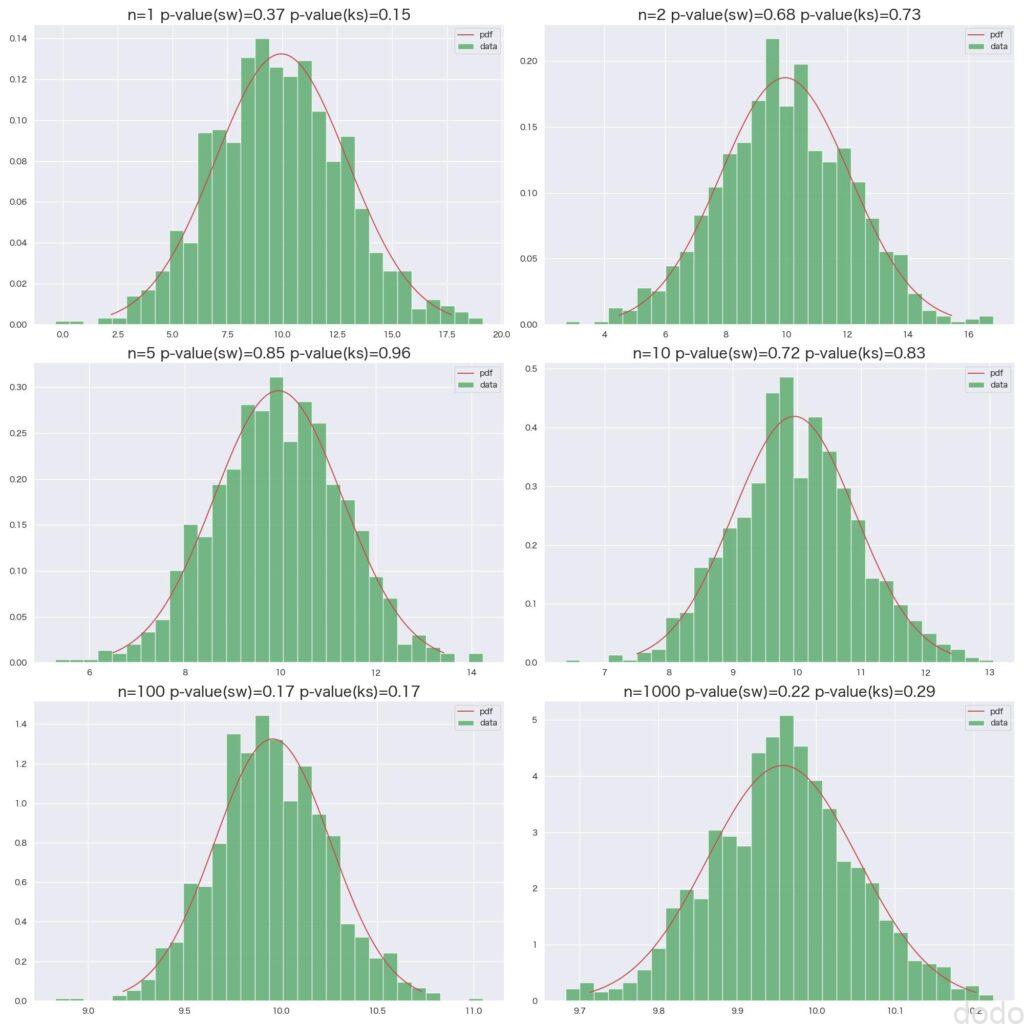正規分布母集団からの標本平均ヒストグラムの形状からもP値からも中心極限定理によく当てはまる（正規分布の帰無仮説を棄却しない）のがわかると思います。（母集団が正規分布なので\(n=1\)でもそれなりに当てはまっています。）
母集団が一様分布の場合
一様分布の母集団から抽出した標本の場合に中心極限定理を確かめてみましょう。
まずは母集団を生成します。
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':20, 'alpha':0.8}
#一様分布を生成
uniform = distribution(stats.uniform,**sts_kwds)
#一様分布を可視化
uniform.plot_hist(**plt_kwds, file_name="uniform_distribute.jpg")
#乱数データを取得
parent_set_uniform = uniform.rvs()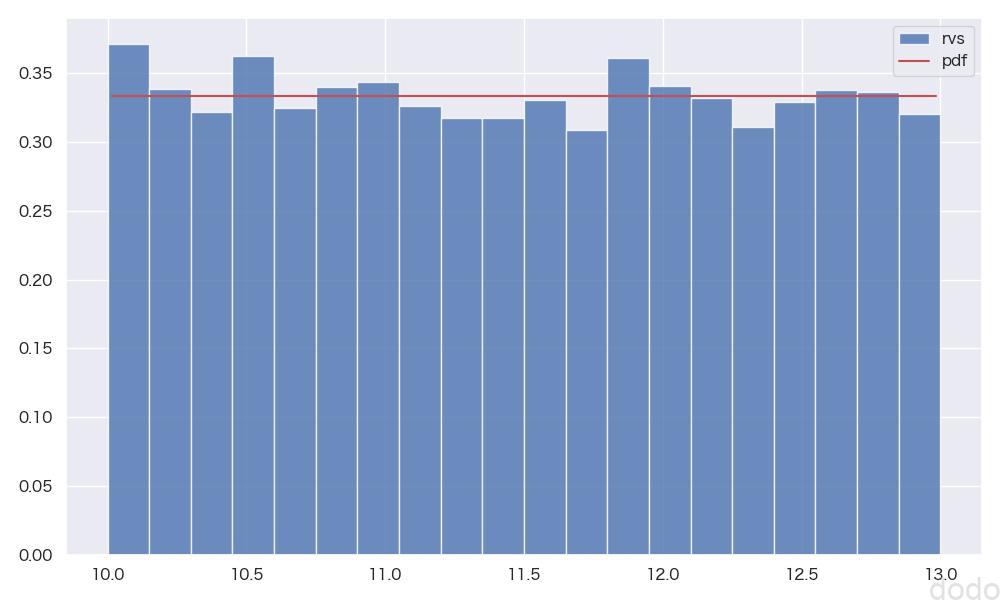
一様分布の母集団（\(X \sim U(10,13)\) ）この母集団をもとに標本のサンプルサイズ1,2,5,10,100,1000毎に1000回の抽出を繰り返してヒストグラムを可視化します。
plot_sample_mean_distribution([1,2,5,10,100,1000],
1000,
parent_set_uniform,
file_name='uniform_sample_mean_hist.jpg')実行すると以下のような結果になります。
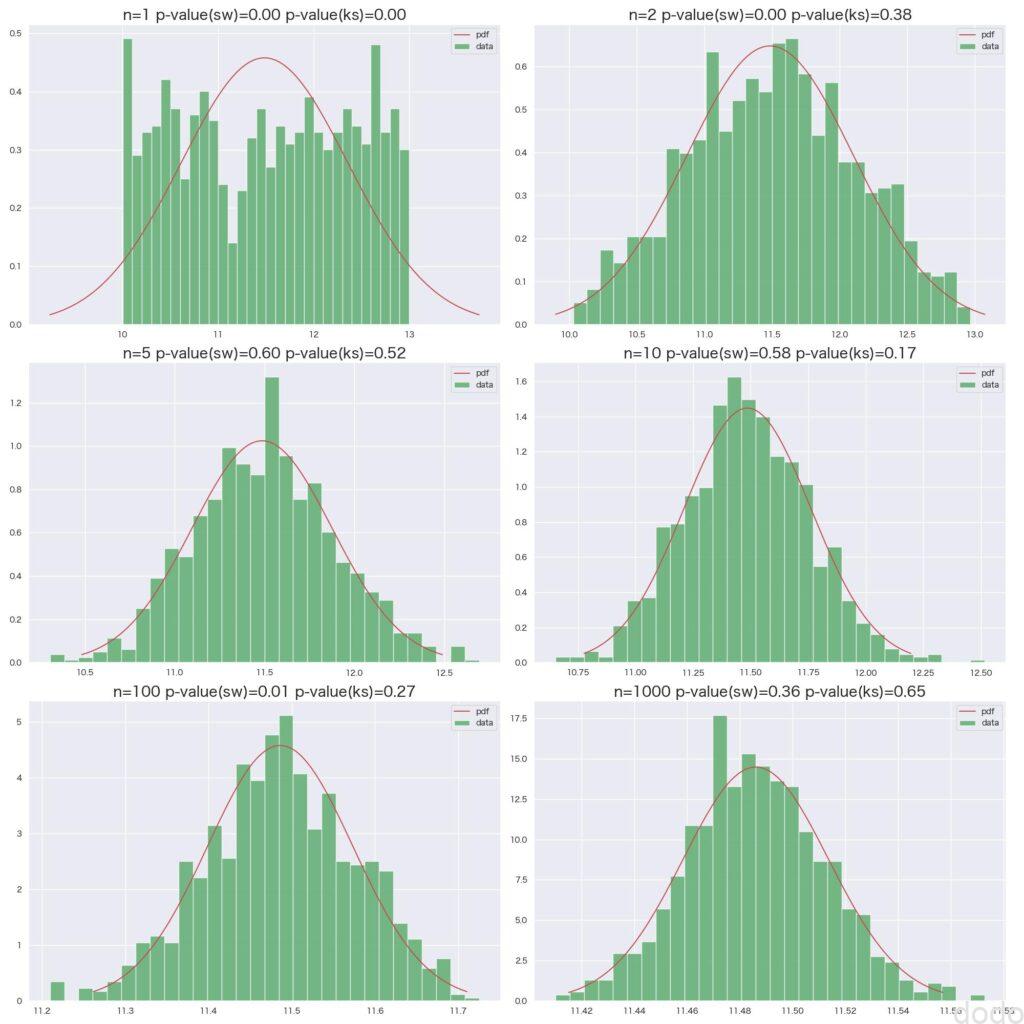一様分布母集団からの標本平均\(n=1\)では一様分布そのものですが、\(n=2\)で既に正規分布に近い形状になっております。（S-W検定では棄却されていますが、K-S検定では正規分布を棄却しない結果になっています。）
\(n\geq 5\)だとおおむね検定上も正規分布を棄却しない結果になっています。（\(n=100\)の場合のみS-W検定で棄却されていますが、何度か繰り返すと棄却されないケースが多いので、たまたま（第一種過誤）かと思います。）
母集団が”変な形の分布”の場合
正規分布、一様分布と続いたら指数分布、ベータ分布・・などと確かめてみたいところです。ただ、これらの分布の中心極限定理の検証は他のサイトでもよく見かけるので、ここでは一足飛びに、分布を混ぜた変な形の分布を作成して、それでも中心極限定理が成立するか確かめてみます。
ここでは指数分布とベータ分布を足し合わせて母集団分布を作成します。
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':20, 'alpha':0.8}
#指数分布
expon = distribution(stats.expon,**sts_kwds)
parent_set_expon = expon.rvs()
#ベータ分布
sts_kwds.update({'a':1.5, 'b':0.75})
beta = distribution(stats.beta,**sts_kwds)
parent_set_beta = beta.rvs()
#指数分布とベータ分布のデータを足し合わせる。
parent_set_mixed = np.append(4 * parent_set_beta, parent_set_expon)
可視化すると以下のようなヒストグラムになります。
plot_hist(parent_set_mixed, "paret_set_mixed.jpg", 30)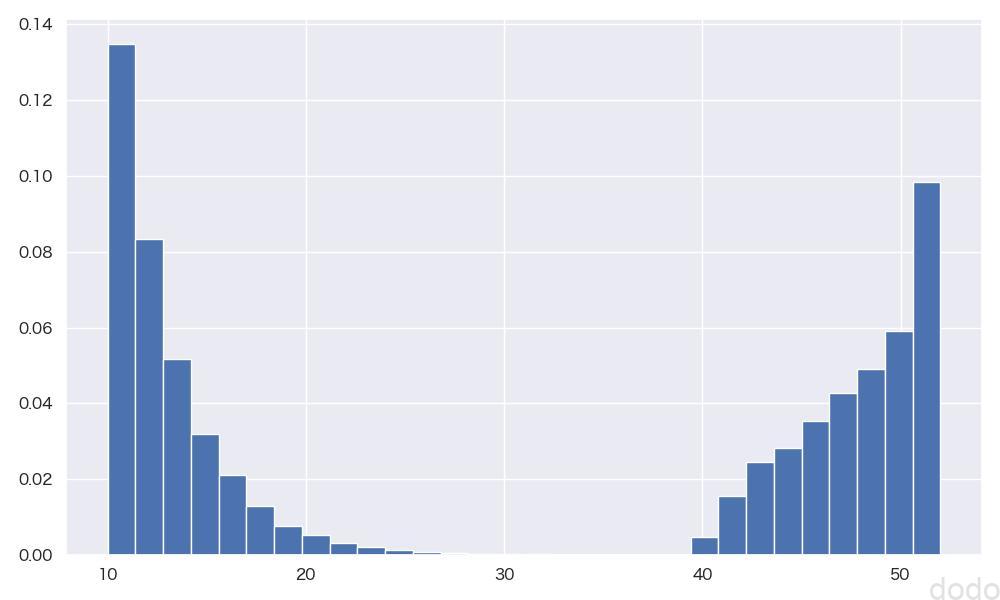
母集団分布(指数分布とベータ分布の混合）この母集団をもとに標本のサンプルサイズ1,2,5,10,100,1000毎に1000回の抽出を繰り返してヒストグラムを可視化します。
plot_sample_mean_distribution([1,2,5,10,100,1000],
1000,
parent_set_mixed,
file_name='mixed_sample_mean.jpg')実行すると以下のような結果になります。
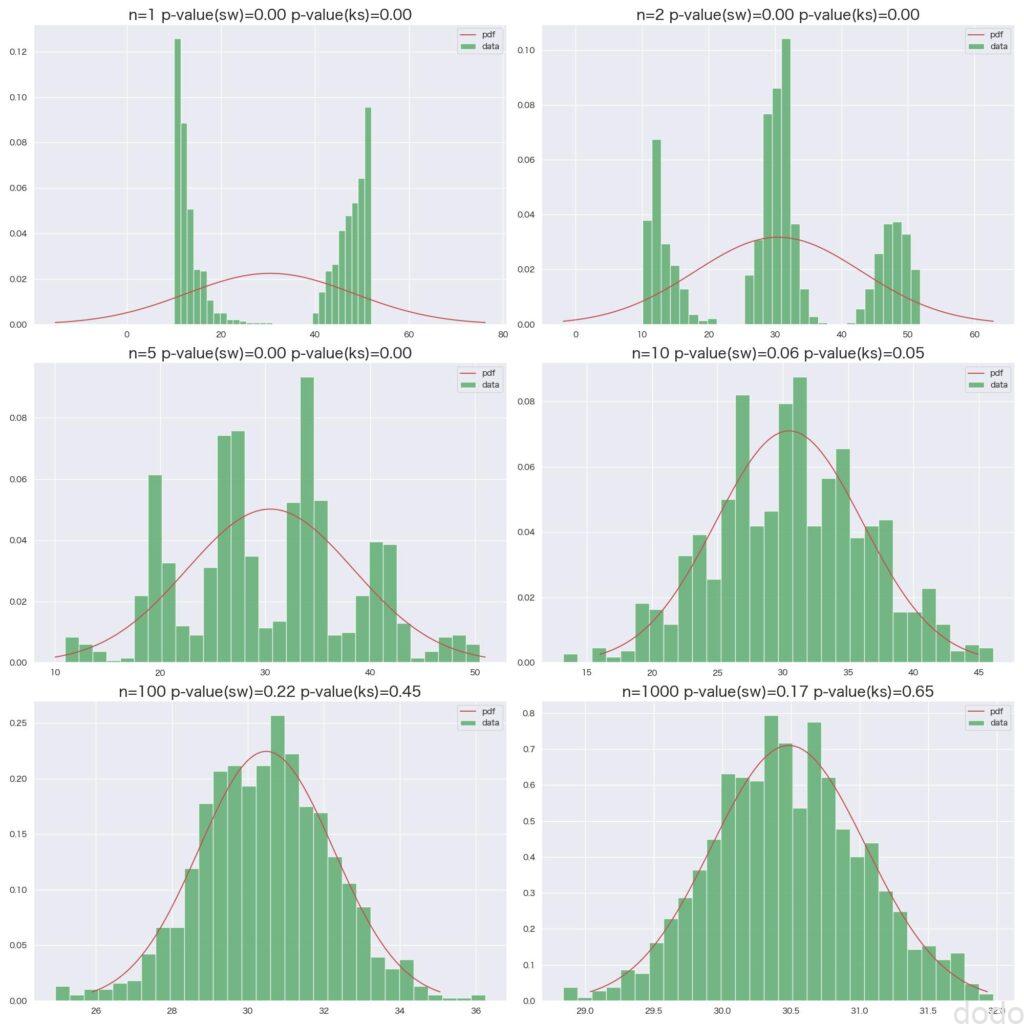混合した母集団からの標本平均ここまで元の分布が歪んだ形だと\(n\)が1桁では正規分布からはかなり遠く、\(n=10\)を超えたあたりからようやく正規分布の形状に近づいてくるのがわかります。
（おまけ）母集団がコーシー分布の場合
冒頭に中心極限定理が成立する条件として、「期待値と分散が求められるような母集団の場合」と記載しました。
コーシー分布は、中心から無限にデータがゆるやかに広がっていくため、期待値と分散が求められません。
最後におまけとして、コーシー分布の母集団から標本を取得したときに、中心極限定理が成立しないことを見ていきましょう。
まずはコーシー分布の母集団を生成します。
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':20, 'alpha':0.8}
#コーシー分布を生成
cauchy = distribution(stats.cauchy, **sts_kwds)
#コーシー分布を可視化
cauchy.plot_hist(**plt_kwds, file_name="cauchy_distribute.jpg")
#乱数データを取得
parent_set_cauchy = cauchy.rvs()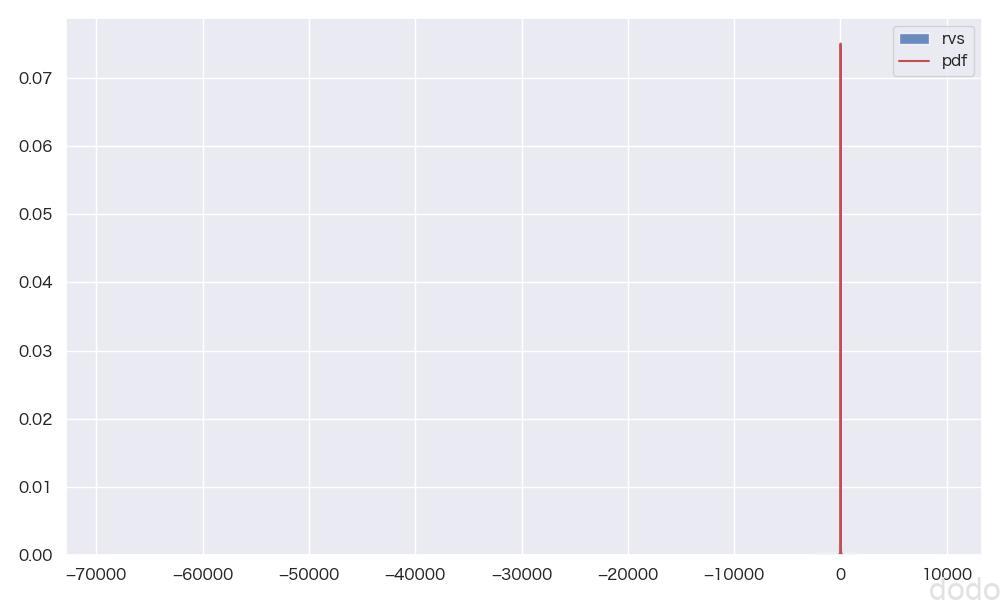
コーシー分布の母集団（裾野が広いためうまく表示できない）データの分布が広すぎて、うまく分布が可視化できていません。
表示範囲を-10から30の間に限定して再表示します。（pdfのプロット数も増やすため、生成からやり直します。）
#statsの引数
sts_kwds = {'loc':10, 'scale':3}
#plot#histの引数
plt_kwds = {'bins':30, 'range':(-10,30), 'alpha':0.8}
#コーシー分布を生成 (pdfの生成点を増やす）
cauchy = distribution(stats.cauchy, **sts_kwds, pdf_x_size=1000)
#コーシー分布を可視化（軸のレンジを限定）
fig, ax = plt.subplots()
ax.set_xlim([-10, 30])
cauchy.plot_hist(**plt_kwds, ax=ax, file_name="cauchy_distribute2.jpg")
#乱数データを取得
parent_set_cauchy = cauchy.rvs()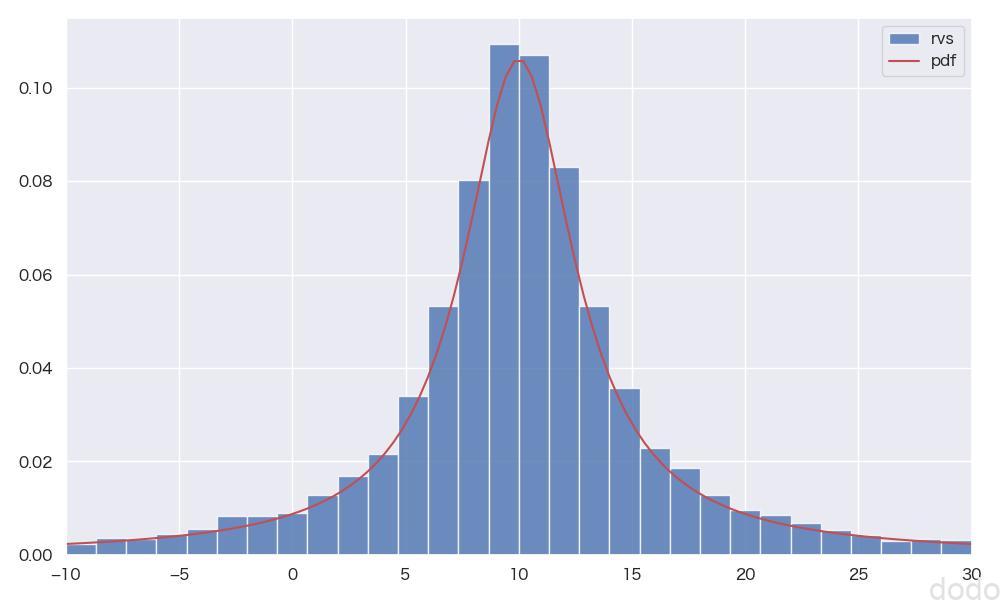
コーシー分布の母集団（表示範囲限定）一見、正規分布に似た形状になっていますが、正規分布に比べて減少がゆるやかになっています。
この母集団をもとに標本のサンプルサイズ1,2,5,10,100,1000毎に1000回の抽出を繰り返してヒストグラムを可視化します。
plot_sample_mean_distribution([1,2,5,10,100,1000],
1000,
parent_set_cauchy,
file_name='cauchy_sample_mean.jpg')実行すると以下のような結果になります。
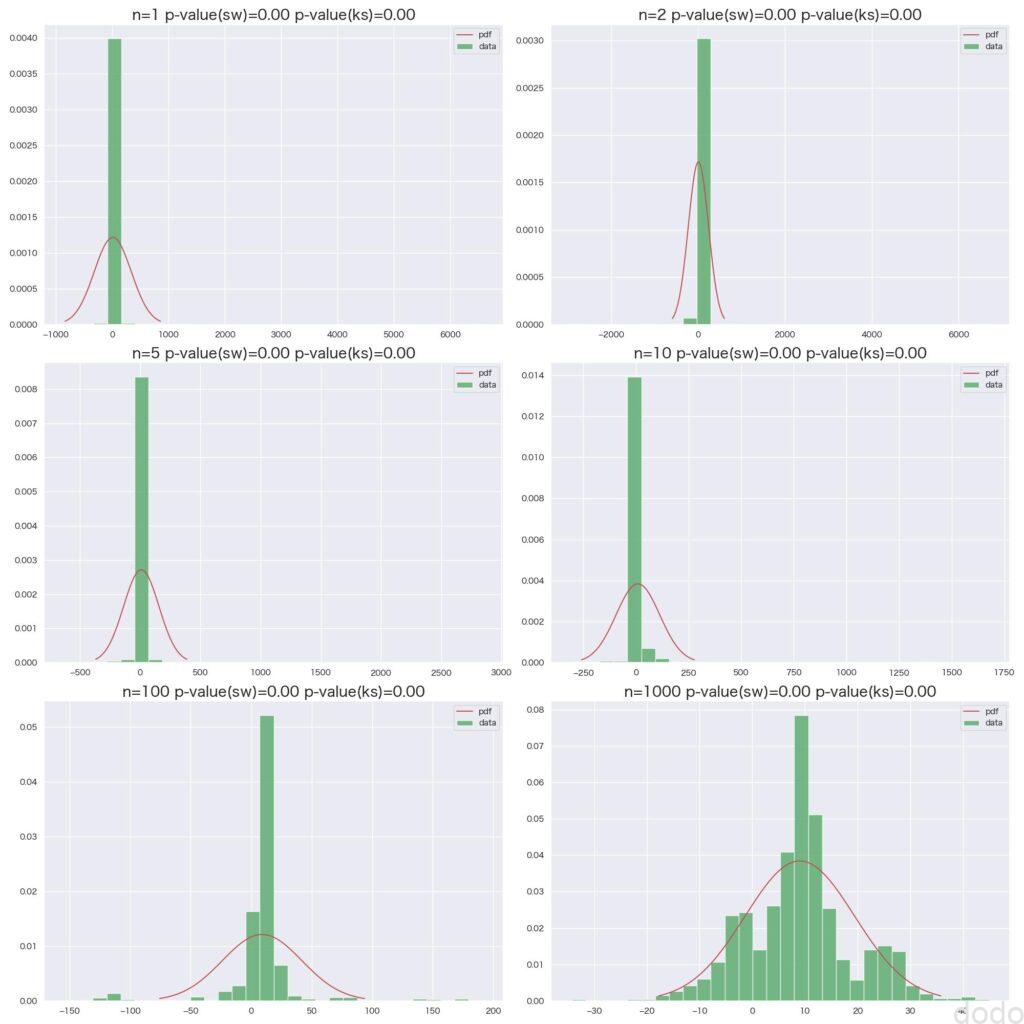コーシー分布母集団からの標本平均サンプルサイズを増やせば、標本平均が取る値の範囲は狭まってきていますが、p値は全て0.00となっており、正規分布とは全く一致していません。このことから母集団がコーシー分布の場合は中心極限定理が成立していないことがわかります。
まとめ
以上、様々な分布の母集団から標本平均を取得して、中心極限定理に従うかどうかを可視化して確認しました。
コーシー分布のような期待値と分散が求められないものを除けば、どのような歪んだ分布であろうと中心極限定理に従うことがわかります。
数式だけだと中心極限定理の意味がピンと来ない人でも、可視化するとこの定理の凄さがわかるのではないでしょうか。
統計の定理などで、数式だけ見た感じだと直感的にわかりにくい場合はこのように具体的に可視化すると良いでしょう。
