以下の記事で、SIRモデルをpythonで実装してみました。
リンク先の記事では、「えいや」で決めた日本での新型コロナの流行を想定したパラメータを元にモデルを作成しましたが、2020/5/20時点、全く実データとマッチしていません。
そこで本記事では、実際に報告されているデータから学習してSIRモデルのパラメータを決定して、今後の動向を予測することを試みてみます。（まあ、収束が見えてきている現在、周回遅れ気味ではありますが・・）
なお、前回の記事と同様、本記事も数理モデルでのデータの学習・予測をpythonで実装する事が目的であり、高い精度で結果を予測するものではないのでご了承ください。（結果に対しては一切の責任も持ちません。）
※2020/9/16追記
第二波が来たので、やっぱり外れました・・・
SEWIR-Fモデルについて
前回のSIRモデルの記事では、通常のSIRモデルと死亡者を考慮したSIR-Fモデルを使用しました。
ただし、新型コロナの特徴として、潜伏期間が長い事と報告が上がってくるまでタイムラグがある事から、実際に感染してから報告されるまで約２週間あるのではないかと言われています。
そこで、本記事では、SIR-Fモデルをさらに拡張したSEWIR-Fモデルというものを使用します。以下に記載されている数式を参考にさせていただきました。
参考リンク：https://www.kaggle.com/lisphilar/covid-19-data-with-sir-model
※参考にしたのは数式のみで掲載されているソースコードに関しては一切、参考・流用しておりません。
SEWIR-Fモデルは\(S\)（感受性保持者）、\(I\)（感染者と判定された者）、\(R\)（免疫保持者）、\(F\)（死亡者）に加えて、\(E\)（感染し潜伏期間の者）、\(W\)（感染し検査結果待ち(報告待ち)の者）が追加され、以下のような微分方程式で表現できます。
\begin{eqnarray}
\frac{dS(t)}{dt} &=&-\beta_{1} S(t) (W(t) + I(t))\\
\frac{dE(t)}{dt} &=&\beta_{1} S(t) (W(t) + I(t)) -\beta_{2}E(t)\\
\frac{dW(t)}{dt} &=&\beta_{2}E(t) – \beta_{3}W(t)\\
\frac{dI(t)}{dt} &=&\beta_{3} (1-\alpha_{1}) W(t) – (\gamma + \alpha_{2}) I(t)\\
\frac{dR(t)}{dt} &=&\gamma I(t)\\
\frac{dF(t)}{dt} &=&\beta_{3} \alpha_{1} W(t) + \alpha_{2} I(t)\\
\end{eqnarray}
フローで表すと以下のようになります。
\begin{eqnarray}
\Large S&\Large\,\overset{\beta_{1} (W + I)}{\rightarrow}\,&\Large W&\Large\,\overset{\beta_2}{\rightarrow}\,&\Large E&\Large\,\overset{\beta_3}{\rightarrow}\,&\Large S^{*}&\Large\,\overset{\alpha_1}{\rightarrow}\,&\Large F\\
&&&&&&\Large &\Large\,\overset{1-\alpha_1}{\rightarrow}\,&\Large I&\Large\,\overset{\gamma}{\rightarrow}\,&\Large R\\
&&&&&&&&&\Large \,\overset{\alpha_2}{\rightarrow}\,&\Large F\\
\end{eqnarray}
なお基本再生産数は以下の式で表されます。
$$\mathcal{R_{0}} = \frac{\beta_1 (1- \alpha_1) S_{0}}{\gamma+\alpha_2} $$
SEWIR-Fモデルの実装
それではSEWIR-Fモデルをpythonで実装してみましょう。
まずは必要なライブラリをインポートします。
import numpy as np
import pandas as pd
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
from datetime import timedelta
import json
import matplotlib.pyplot as plt
%matplotlib inline
前回のSIRモデルの記事と同様にsolve_ivpに渡すための常微分方程式を実装したcallback関数を定義します。
def SEWIRF_wrapper(alpha1, alpha2, beta1, beta2, beta3, gamma):
def SEWIRF(t, y):
s,e,w,i,r,f = y[0],y[1],y[2],y[3],y[4],y[5]
ds = - beta1 * s * (w + i)
de = beta1 * s * (w + i) - beta2 * e
dw = beta2 * e - beta3 * w
di = (1 - alpha1) * beta3 * w - (gamma + alpha2) * i
dr = gamma * i
df = alpha1 * beta3 * w + alpha2 * i
return [ds, de, dw, di, dr, df]
return SEWIRFとりあえずプロットする。
とりあえず適当な初期値を用いてモデルをプロットするための関数を実装します。
def try_SEWIRF(T=365, S_0=126000000, R0=2.5, recover_date=14,latent_date=5, judge_date=8, mortal_rate=0.02):
#トレース時間(日)
#T = 600
#感受性保持者初期値(人口)
#S_0 = 126000000
#潜在感染者初期値
E_0 = 1
#待機者初期値
W_0 = 0
#感染者初期値
I_0 = 0
#回復者初期値
R_0 = 0
#死者
F_0 = 0
#判定前死亡率（無視できる範囲とする）
alpha1 = 0
#回復期間(または死亡するまでの期間）
gamma = 1 / recover_date
#致死率
alpha2 = gamma * mortal_rate / (1 - mortal_rate)
#潜伏期間の逆数
beta2 = 1 / latent_date
#判定待ち期間の逆数
beta3 = 1 / judge_date
#感染率
beta1 = R0 * (gamma + alpha2) / S_0 / (1 - alpha1)
result = solve_ivp(SEWIRF_wrapper(alpha1, alpha2, beta1, beta2, beta3, gamma),
[0, T],
[S_0, E_0, W_0, I_0, R_0, F_0],
t_eval=np.arange(0, T))
confirmed_total = result.y[3] + result.y[4] + result.y[5]
recover_total = result.y[4]
death_total = result.y[5]
confirmed_daily = np.diff(confirmed_total)
recover_daily = np.diff(recover_total)
death_daily = np.diff(death_total)
#plot
fig = plt.figure(figsize=(16, 5))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title(f"SEWIR-Fモデル(累計) R0={R0}", fontsize=16)
ax1.set_xlabel("日数",fontsize=15)
ax1.set_ylabel("人数",fontsize=15)
ax1.plot(result.t,result.y[0],label='感受性保持者数')
ax1.plot(result.t,confirmed_total,label='感染者数')
ax1.plot(result.t,result.y[3],label='患者数')
ax1.plot(result.t,recover_total,label='回復者数')
ax1.plot(result.t,death_total,label='死亡者数')
ax1.legend(fontsize=15)
ax2 = fig.add_subplot(1,2,2)
ax2.set_title(f"SEWIR-Fモデル(新規) R0={R0}", fontsize=16)
ax2.set_xlabel("日数",fontsize=15)
ax2.set_ylabel("人数",fontsize=15)
ax2.plot(result.t[:-1],confirmed_daily,label='感染者数')
ax2.plot(result.t[:-1],recover_daily,label='回復者数')
ax2.plot(result.t[:-1],death_daily,label='死亡者数')
ax2.legend(fontsize=15)
plt.savefig(f"./SEWIRF_try_{R0}.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
ソース上、表示期間は365日、感受性保持者は日本の人口の126,000,000人、回復期間（または死亡するまでの期間）を14日、潜伏期間を5日、検査してから感染者と判定されるまでの期間を8日、感染者の致死率を2%としています。（※なお感染者に判定される前の死亡率は無視できるものとして０としています。）
基本再生産数の\(\mathcal{R_{0}}\)を2.5と1.7の場合について可視化します。
try_SEWIRF(R0=2.5)
try_SEWIRF(R0=1.7)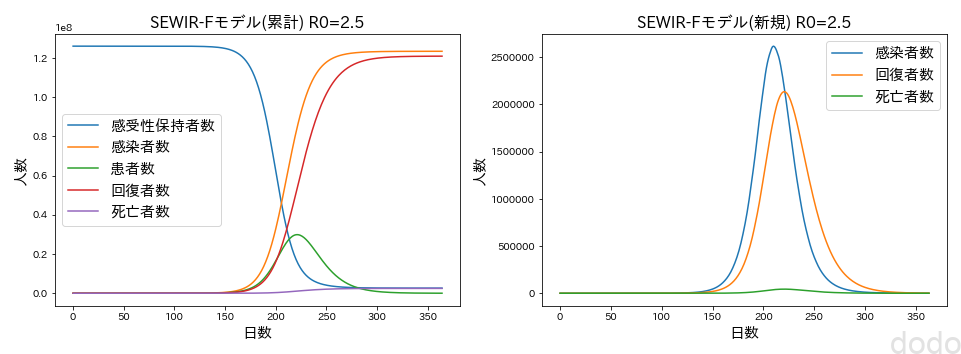
SEWIRFお試し(R0=2.5)
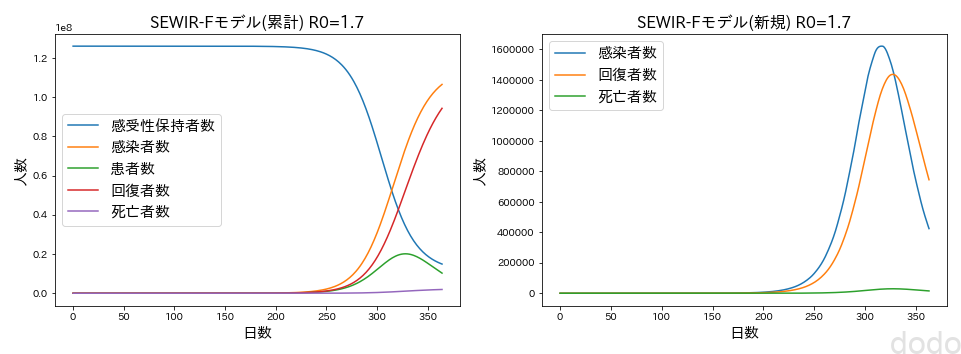SEWIRFお試し(R0=1.7)左が常微分方程式を解いた結果を可視化したデータで、右がそのデータの差分を取ることにより1日ごとのデータに変換して可視化したものとなります。
なおグラフ上の「患者数」は、\(I\)であり、「感染者数」は\(I+R+F\) となります。
パラメータを変えてプロットする。
次に１つのグラフ上でパラメータを変えたものをプロットします。
以下にパラメータを変えて呼び出せるようにしたSEWIR-Fモデルを解く関数とデータをプロットするための関数を実装します。
def simulate_SEWIRF(T=360, #トレース時間(日)
S_0=126000000, #感受性保持者初期値
E_0=1, #潜在感染者初期値
W_0=0, #待機者初期値
I_0=0, #感染者初期値
R_0=0, #回復者初期値
F_0=0, #死者
R0=2.5, #基本再生産数
recover_date=14, #平均回復日数
latent_date=5, #潜伏期間
judge_date=8, #判定（報告）期間
mortal_rate=0.02 #死亡率
):
#判定前死亡率（無視できる範囲とする）
alpha1 = 0
#回復期間(または死亡するまでの期間）
gamma = 1 / recover_date
#致死率
alpha2 = gamma * mortal_rate / (1 - mortal_rate)
#潜伏期間の逆数
beta2 = 1 / latent_date
#判定待ち期間の逆数
beta3 = 1 / judge_date
#感染率
beta1 = R0 * (gamma + alpha2) / S_0 / (1 - alpha1)
result = solve_ivp(SEWIRF_wrapper(alpha1, alpha2, beta1, beta2, beta3, gamma),
[0, T],
[S_0, E_0, W_0, I_0, R_0, F_0],
t_eval=np.arange(0, T))
return result
def plot_SEWIRF(params_list,file_suffix):
fig = plt.figure(figsize=(16, 12))
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(f"SEWIR-Fモデル 感染者数(累計)", fontsize=16)
ax1.set_xlabel("日数",fontsize=15)
ax1.set_ylabel("人数",fontsize=15)
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(f"SEWIR-Fモデル 感染者数(新規)", fontsize=16)
ax2.set_xlabel("日数",fontsize=15)
ax2.set_ylabel("人数",fontsize=15)
ax3 = fig.add_subplot(2,2,3)
ax3.set_title(f"SEWIR-Fモデル 死亡者数(累計)", fontsize=16)
ax3.set_xlabel("日数",fontsize=15)
ax3.set_ylabel("人数",fontsize=15)
ax4 = fig.add_subplot(2,2,4)
ax4.set_title(f"SEWIR-Fモデル 死亡者数(新規)", fontsize=16)
ax4.set_xlabel("日数",fontsize=15)
ax4.set_ylabel("人数",fontsize=15)
for params in params_list:
result = simulate_SEWIRF(**params)
confirmed_total = result.y[3] + result.y[4] + result.y[5]
death_total = result.y[5]
confirmed_daily = np.diff(confirmed_total)
death_daily = np.diff(death_total)
ax1.plot(confirmed_total,label=json.dumps(params))
ax1.annotate("{:,.0f}".format(confirmed_total[-1]), xy = (result.t[-1], confirmed_total[-1]),fontsize=10)
ax2.plot(confirmed_daily,label=json.dumps(params))
ax2.annotate("{:,.0f}".format(confirmed_daily[-1]), xy = (result.t[-1], confirmed_daily[-1]),fontsize=10)
ax3.plot(death_total,label=json.dumps(params))
ax3.annotate("{:,.0f}".format(death_total[-1]), xy = (result.t[-1], death_total[-1]),fontsize=10)
ax4.plot(death_daily,label=json.dumps(params))
ax4.annotate("{:,.0f}".format(death_daily[-1]), xy = (result.t[-1], death_daily[-1]),fontsize=10)
ax1.legend(fontsize=10)
ax2.legend(fontsize=10)
ax3.legend(fontsize=10)
ax4.legend(fontsize=10)
plt.savefig(f"./SEWIRF_simulate_{file_suffix}.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
まずは、基本再生産数を1.5、2、2.5と変えてプロットしてみます。
params_list = [
dict(S_0=126000000,R0=2.5),
dict(S_0=126000000,R0=2),
dict(S_0=126000000,R0=1.5),
]
plot_SEWIRF(params_list,"case1")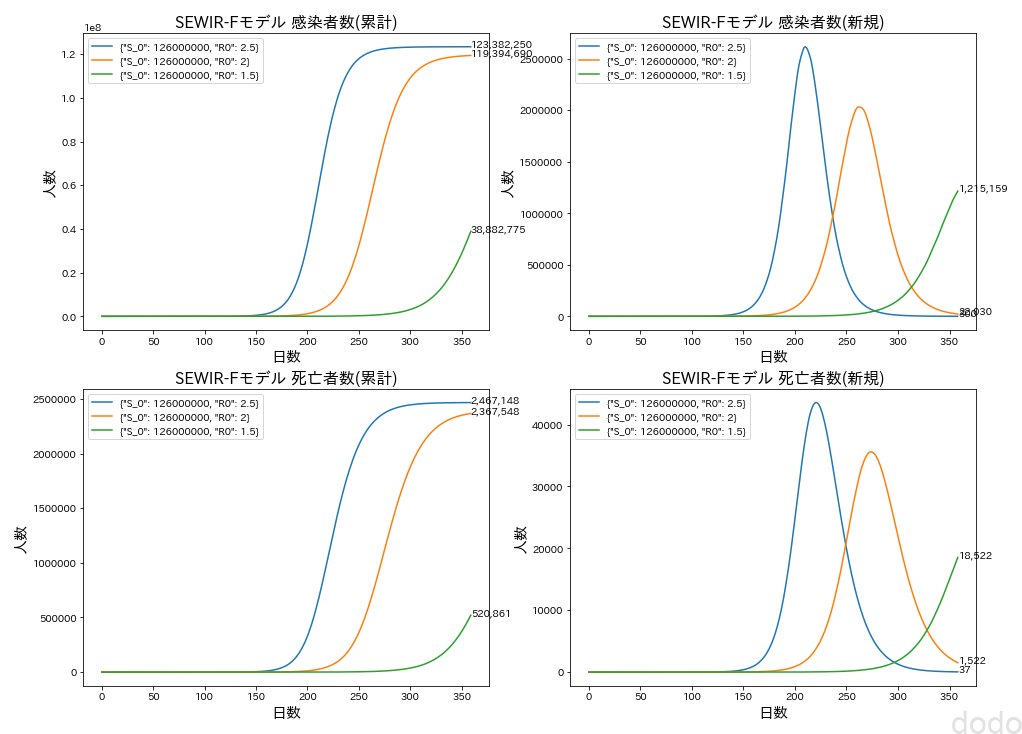
SEWIRFモデル（R0=2.5,2,1,5)基本再生産数を小さくするほどピークが未来にずれます。ただ基本再生産数を変更しただけでは、実際のデータへのフィットは難しそうです。
次は基本再生産数を2に固定して、感受性保持者数を変えてプロットします。（自然免疫を持っている人が多くて、感染する人が少ない可能性があるため）
params_list = [
dict(S_0=126000000,R0=2),
dict(S_0=10000000,R0=2),
dict(S_0=1000000,R0=2),
]
plot_SEWIRF(params_list,"case2")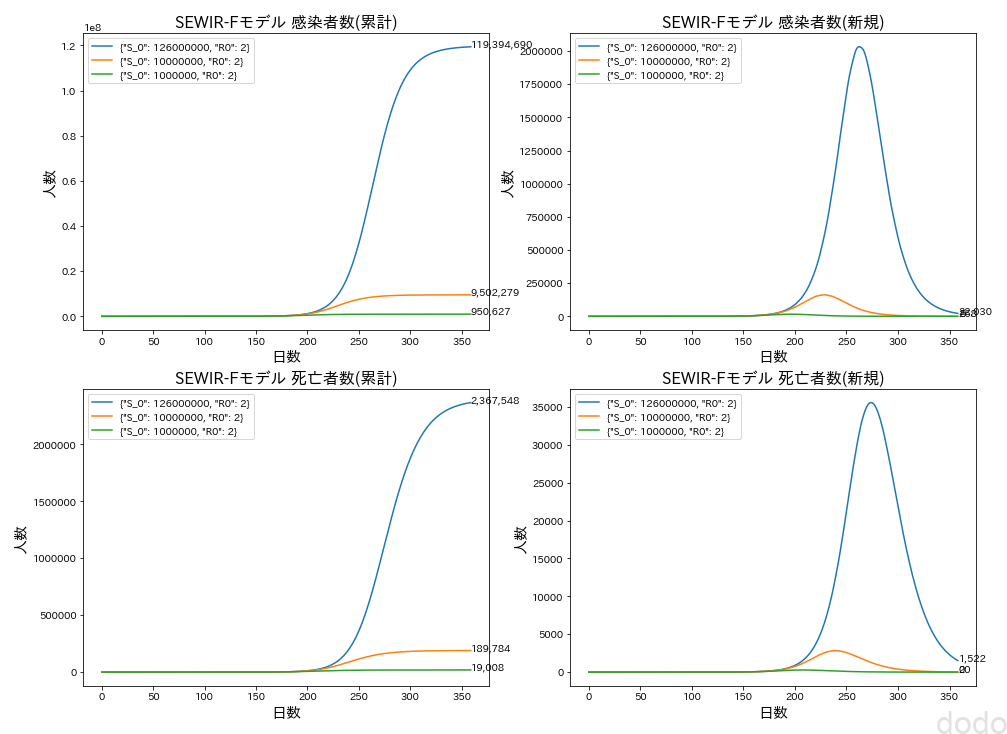
SEWIRFモデル（S_0=10^8,10^7,10^6)感受性保持者を少なくすれば、死亡者数は減っていきます。ただし100万人以下（人口の1%以下）とするのはそれはそれで少なすぎる気がするので、次は致死率を変えてプロットしてみます。
params_list = [
dict(S_0=1000000,R0=2,mortal_rate=0.05),
dict(S_0=1000000,R0=2,mortal_rate=0.02),
dict(S_0=1000000,R0=2,mortal_rate=0.01),
]
plot_SEWIRF(params_list,"case3")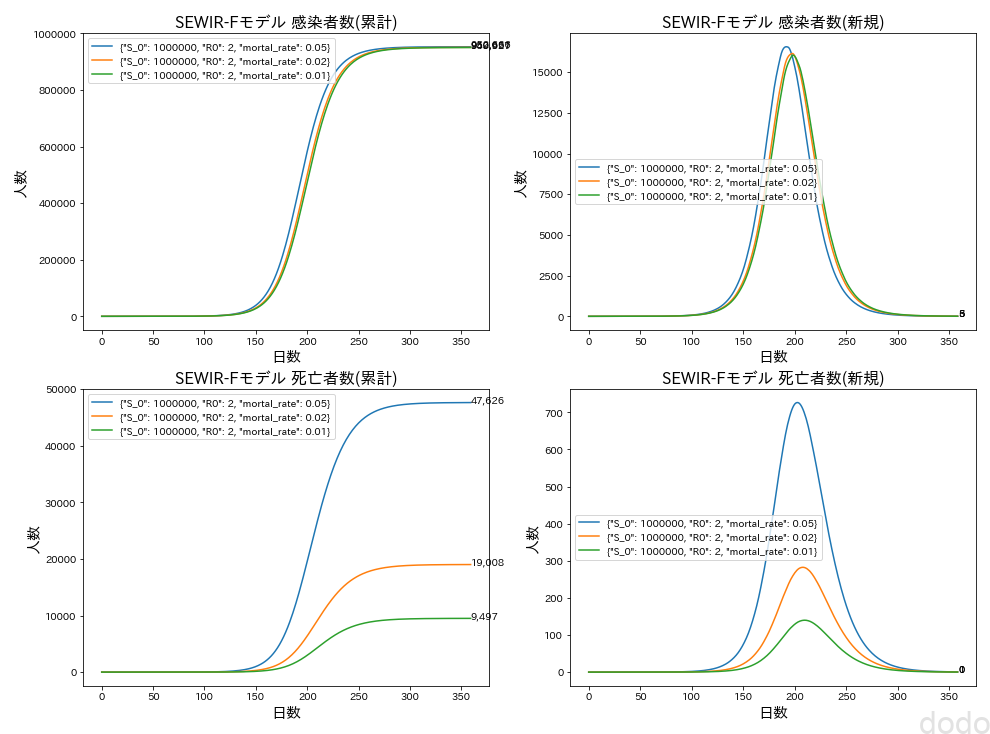
SEWIRFモデル(致死率5%,2%,1%)死亡者数は減りましたが、まだ実際の報告値とはかけはなれています。また、感染者数の傾向は致死率を変えても大きくは変わりません。
SEWIR-Fモデルと実データと比較する。
前回の記事や前節では、SEWIR-Fモデルでパラメータを変えた結果のみを可視化していました。
ただ、このままでは机上の空論なので、まずは実データと比較して、どのくらい差異があるかを可視化します。
まずは実データをwgetで取得します。
wget https://github.com/kaz-ogiwara/covid19/raw/master/data/summary.csvデータは、東洋経済オンラインのコロナ感染状況のためのデータを使用させていただきました。(※現在、生データの公開は停止されています。）
データの細かい詳細については省略します。
欠損している日付を前日データで埋めて、必要な列（日付、感染者数(PCR陽性者数）、退院者数、死亡者数）のみに絞り込みます。
#読み込み
covid_data = pd.read_csv("./summary.csv")
#日付を変換
covid_data["date"] = covid_data["year"].astype(str) +"/"+ covid_data["month"].astype(str) +"/"+ covid_data["date"].astype(str)
covid_data["date"] = pd.to_datetime(covid_data["date"])
covid_data = covid_data.drop(["year","month"],axis=1)
#日付欠損埋め
start_datetime = covid_data["date"].iloc[0]
end_datetime = covid_data["date"].iloc[-1]
periods = (end_datetime-start_datetime).days + 1
date_df = pd.DataFrame({"date":[start_datetime + timedelta(days=i) for i in range(periods)]})
covid_data = pd.merge(date_df, covid_data, on="date", how="left")
#列を絞り込む
covid_data = covid_data[["date","pcr_tested_positive","discharged","death"]]
#欠損値を前日日付で埋める
null_df = covid_data[covid_data.isnull().any(axis=1)]
for index, row in null_df.iterrows():
covid_data["pcr_tested_positive"].iloc[index] = covid_data["pcr_tested_positive"].iloc[index-1]
covid_data["discharged"].iloc[index] = covid_data["discharged"].iloc[index-1]
covid_data["death"].iloc[index] = covid_data["death"].iloc[index-1]
以下のコードで感染データを可視化します。
#plot
fig = plt.figure(figsize=(16, 6))
date_fmt = covid_data["date"].apply(lambda x:x.strftime("%-m/%-d"))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title("感染者数(累計)", fontsize=16)
ax1.plot(date_fmt,covid_data["pcr_tested_positive"],label="感染者数")
ax1.plot(date_fmt,covid_data["discharged"],label="退院者数")
ax1.plot(date_fmt,covid_data["death"],label="死亡者数")
ax1.grid(which="both",axis='x')
ax1.set_xticks(np.arange(0,len(date_fmt),7))
ax1.set_xlabel("日付",fontsize=15)
ax1.set_ylabel("人数",fontsize=15)
ax1.legend(fontsize=10)
ax2 = fig.add_subplot(1,2,2)
ax2.set_title("感染者数(新規)", fontsize=16)
ax2.plot(date_fmt,covid_data["pcr_tested_positive"].diff(),label="感染者数")
ax2.plot(date_fmt,covid_data["discharged"].diff(),label="退院者数")
ax2.plot(date_fmt,covid_data["death"].diff(),label="死亡者数")
ax2.grid(which="both",axis='x')
ax2.set_xticks(np.arange(0,len(date_fmt),7))
ax2.set_xlabel("日付",fontsize=15)
ax2.set_ylabel("人数",fontsize=15)
ax2.legend(fontsize=10)
plt.savefig(f"./covid19_japan_plot.png",bbox_inches='tight', pad_inches=0.2)
plt.show()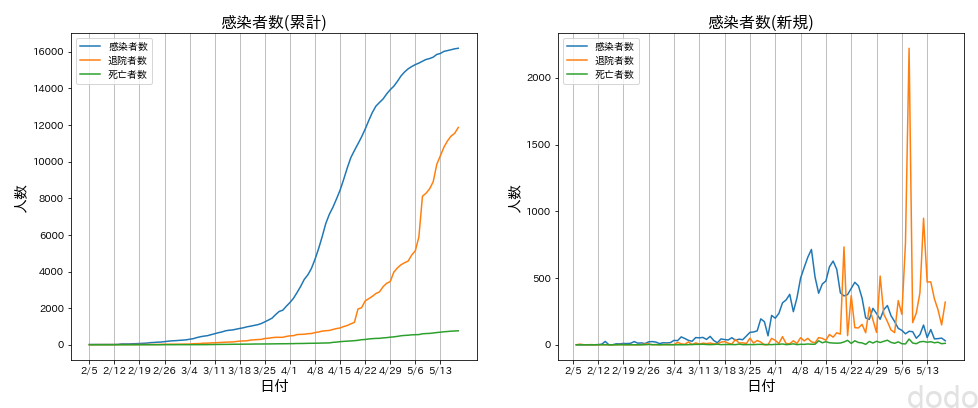
新型コロナ感染状況（日本）可視化したデータから以下の事がわかります。
- 感染者数（報告時点）は４月初旬から急激に上昇している。
- 新規の感染者数は４月半ば（報告時点）をピークに減少している。
- ４月中旬から退院者数が増加している。
それではSEWIR-Fモデルの結果と合わせて可視化します。（可視化コードは以下の通り）
def plot_SEWIRF_compare(covid_data,params_list,file_suffix,forecast_day =50):
start_datetime = covid_data["date"].iloc[0]
end_datetime = covid_data["date"].iloc[-1]
report_periods = (end_datetime-start_datetime).days + 1
forecast_periods = report_periods + forecast_day
report_dates =[(start_datetime + timedelta(days=i)).strftime("%-m/%-d") for i in range(report_periods)]
forecast_dates =[(start_datetime + timedelta(days=i)).strftime("%-m/%-d") for i in range(forecast_periods)]
fig = plt.figure(figsize=(16, 12))
ax1 = fig.add_subplot(2,2,1)
ax1.set_title(f"SEWIR-Fモデル 感染者数(累計)", fontsize=16)
ax1.set_xlabel("日付",fontsize=15)
ax1.set_ylabel("人数",fontsize=15)
ax1.set_xticks(np.arange(0,forecast_periods,15))
ax2 = fig.add_subplot(2,2,2)
ax2.set_title(f"SEWIR-Fモデル 感染者数(新規)", fontsize=16)
ax2.set_xlabel("日付",fontsize=15)
ax2.set_ylabel("人数",fontsize=15)
ax2.set_xticks(np.arange(0,forecast_periods,15))
ax3 = fig.add_subplot(2,2,3)
ax3.set_title(f"SEWIR-Fモデル 死亡者数(累計)", fontsize=16)
ax3.set_xlabel("日付",fontsize=15)
ax3.set_ylabel("人数",fontsize=15)
ax3.set_xticks(np.arange(0,forecast_periods,15))
ax4 = fig.add_subplot(2,2,4)
ax4.set_title(f"SEWIR-Fモデル 死亡者数(新規)", fontsize=16)
ax4.set_xlabel("日付",fontsize=15)
ax4.set_ylabel("人数",fontsize=15)
ax4.set_xticks(np.arange(0,forecast_periods,15))
#初期値は実データから取得
params_common = dict(
T = forecast_periods,
E_0=covid_data["pcr_tested_positive"].iloc[13],
W_0=covid_data["pcr_tested_positive"].iloc[8],
I_0=covid_data["pcr_tested_positive"].iloc[0]-covid_data["discharged"].iloc[0]-covid_data["death"].iloc[0],
R_0=covid_data["discharged"].iloc[0],
F_0=covid_data["death"].iloc[0],
)
# print(params_common)
for params in params_list:
params_common.update(params)
result = simulate_SEWIRF(**params_common)
confirmed_total = result.y[3] + result.y[4] + result.y[5]
death_total = result.y[5]
confirmed_daily = np.diff(confirmed_total)
death_daily = np.diff(death_total)
confirmed_daily_report = covid_data["pcr_tested_positive"].diff()
death_daily_report = covid_data["death"].diff()
ax1.plot(forecast_dates,confirmed_total,label=json.dumps(params))
ax1.annotate("{:,.0f}".format(confirmed_total[-1]), xy = (result.t[-1], confirmed_total[-1]),fontsize=10)
ax2.plot(forecast_dates[1:],confirmed_daily,label=json.dumps(params))
ax2.annotate("{:,.0f}".format(confirmed_daily[-1]), xy = (result.t[-1], confirmed_daily[-1]),fontsize=10)
ax3.plot(forecast_dates,death_total,label=json.dumps(params))
ax3.annotate("{:,.0f}".format(death_total[-1]), xy = (result.t[-1], death_total[-1]),fontsize=10)
ax4.plot(forecast_dates[1:],death_daily,label=json.dumps(params))
ax4.annotate("{:,.0f}".format(death_daily[-1]), xy = (result.t[-1], death_daily[-1]),fontsize=10)
ax1.plot(report_dates,covid_data["pcr_tested_positive"],label="報告値")
ax1.annotate("{:,.0f}".format(covid_data["pcr_tested_positive"].iloc[-1]),
xy = (report_dates[-1], (covid_data["pcr_tested_positive"].iloc[-1])),fontsize=10)
ax2.plot(report_dates[1:],confirmed_daily_report[1:],label="報告値")
ax2.annotate("{:,.0f}".format(confirmed_daily_report.iloc[-1]),
xy = (report_dates[-1], (confirmed_daily_report.iloc[-1])),fontsize=10)
ax3.plot(report_dates,covid_data["death"],label="報告値")
ax3.annotate("{:,.0f}".format(covid_data["death"].iloc[-1]),
xy = (report_dates[-1], (covid_data["death"].iloc[-1])),fontsize=10)
ax4.plot(report_dates[1:],death_daily_report[1:],label="報告値")
ax4.annotate("{:,.0f}".format(death_daily_report.iloc[-1]),
xy = (report_dates[-1], (death_daily_report.iloc[-1])),fontsize=10)
ax1.legend(fontsize=10)
ax2.legend(fontsize=10)
ax3.legend(fontsize=10)
ax4.legend(fontsize=10)
plt.savefig(f"./SEWIRF_compare_{file_suffix}.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
感受性保持者は1,000,000人、基本再生産数は1.5で固定して、致死率は5%、2%、1%の場合で可視化します。
params_list = [
dict(S_0=1000000,R0=1.5,mortal_rate=0.05),
dict(S_0=1000000,R0=1.5,mortal_rate=0.02),
dict(S_0=1000000,R0=1.5,mortal_rate=0.01),
]
plot_SEWIRF_compare(covid_data,params_list,file_suffix="case2")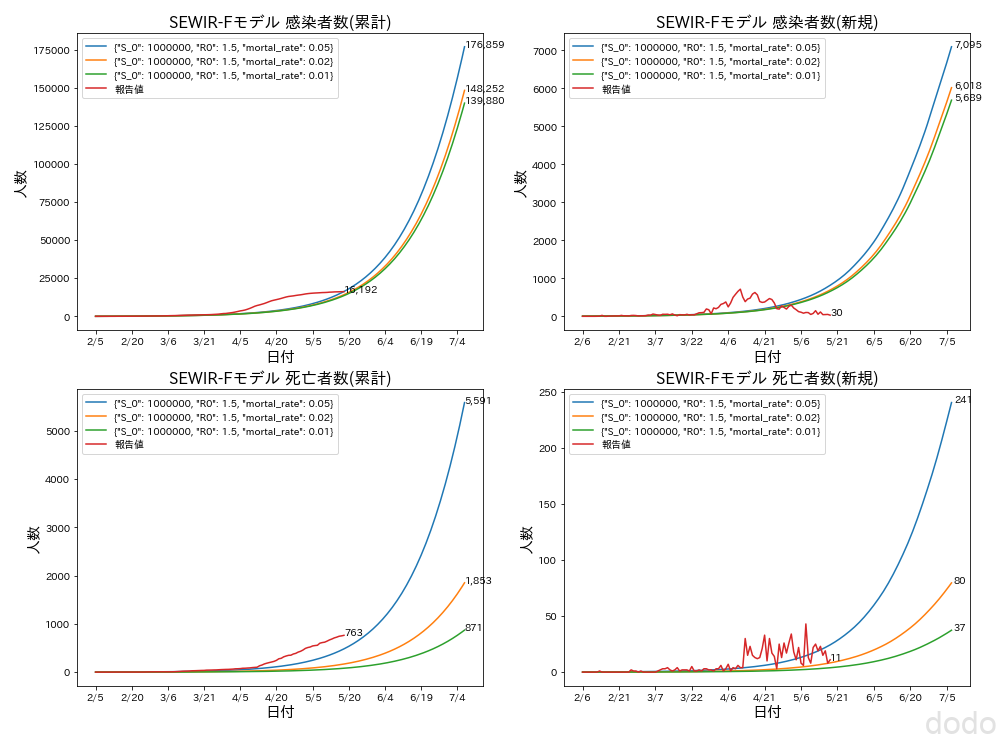
SEWIRFモデル・報告値比較SEWIR-Fモデルの結果は、４月初旬から実データと大きく乖離しているのがわかります。
SEWIR-Fモデルを実データで学習させる。
いよいよSEWIR-Fモデルを実際のデータから学習させてパラメータを決定しましょう。
具体的には、最小二乗法で定義した損失関数を最小にするようなパラメータを求めます。
本来ならば、\(I\)、\(R\)、\(F\)それぞれに対して損失を求めて最小にするようなロジックにするべきですが、実際の報告データに修正がちょくちょく入っており、特に退院者数は微妙な値となっています。（家庭内待機者との区別もよくわからず、また４月半ばの急増は報告漏れを追加したのではとの疑いが・・）
よって損失関数は、感染者数\(I+R+F\)、死亡者数\(F\)のそれぞれで差を最小にするように求めます。
以下、scipy.optimizeのminimizeを使用して最適なパラメータを求めるためのクラスとなります。（コードの詳細については説明を省きます。）
class SEWIRF_estimator(object):
'''
SIRモデルで学習・予測をするためのクラス。
'''
def __init__(self, initial_values,ratio=0.5):
self.initial_values = initial_values
self.ratio = ratio
@staticmethod
def SEWIRF(y,S_0,R0,recover_date,latent_date,judge_date,mortal_rate):
'''
SEWIR-Fモデルの微分方程式の結果を返す。
'''
#判定前死亡率（無視できる範囲とする）
alpha1 = 0
#回復期間(または死亡するまでの期間）の逆数
gamma = 1 / recover_date
#致死率
alpha2 = gamma * mortal_rate / (1 - mortal_rate)
#潜伏期間の逆数
beta2 = 1 / latent_date
#判定待ち期間の逆数
beta3 = 1 / judge_date
#感染率
beta1 = R0 * (gamma + alpha2) / S_0 / (1 - alpha1)
s,e,w,i,r,f = y[0],y[1],y[2],y[3],y[4],y[5]
ds = - beta1 * s * (w + i)
de = beta1 * s * (w + i) - beta2 * e
dw = beta2 * e - beta3 * w
di = (1 - alpha1) * beta3 * w - (gamma + alpha2) * i
dr = gamma * i
df = alpha1 * beta3 * w + alpha2 * i
return [ds, de, dw, di, dr, df]
def predict(self, day_max):
'''
学習したパラメータで予測をする。
'''
def SEWIRF(t, y):
return self.SEWIRF(y, self.S_0, self.R0, self.recover_date, self.latent_date, self.judge_date, self.mortal_rate)
initial_values = [self.S_0] + self.initial_values
return solve_ivp(SEWIRF, [0, day_max], initial_values, t_eval=np.arange(0, day_max))
def loss(self, params, confirmed, deathts):
'''
損失を取得する。
'''
rmse_confirmed,rmse_deaths = self.rmse(params, confirmed, deathts)
loss_value = self.ratio * rmse_confirmed + (1-self.ratio) * rmse_deaths
#収束を見るためにロスを出力
#print(f"loss={loss_value}")
return loss_value
def rmse(self, params, confirmed, deathts, validate_orign=0):
'''
感染者数、死者数のRMSEを取得する。
'''
data_size = validate_orign + len(confirmed)
S_0, R0, recover_date, latent_date, judge_date, mortal_rate = params
def SEWIRF(t, y):
return self.SEWIRF(y, S_0, R0, recover_date, latent_date, judge_date, mortal_rate)
initial_values = [S_0] + self.initial_values
sol = solve_ivp(SEWIRF, [0, data_size], initial_values, t_eval=np.arange(0, data_size), vectorized=True)
rmse_confirmed = np.sqrt(np.mean((sol.y[3][validate_orign:] + sol.y[4][validate_orign:] + sol.y[5][validate_orign:] - confirmed)**2))
rmse_deaths = np.sqrt(np.mean((sol.y[5][validate_orign:] - deathts)**2))
return rmse_confirmed,rmse_deaths
def fit(self, confirmed, deathts):
'''
学習してパラメータをフィットする。
'''
optimal = minimize(
self.loss,
[1000000, 2.5, 14, 5, 8, 0.01],
args=(confirmed, deathts),
method='L-BFGS-B',
bounds=[(10000,10000000), (0.001, 4), (5,30), (1, 10), (3, 10), (0.0001, 0.1)]
)
self.S_0, self.R0, self.recover_date, self.latent_date, self.judge_date, self.mortal_rate = optimal.x
実装したクラスを使用して、可視化するための関数を定義します。
def plot_SEWIRF_predicted(covid_data,fit_period,file_suffix,forecast_day,ratio=0.5):
start_datetime = covid_data["date"].iloc[0]
end_datetime = covid_data["date"].iloc[-1]
report_periods = (end_datetime-start_datetime).days + 1
forecast_periods = report_periods + forecast_day
report_dates =[(start_datetime + timedelta(days=i)).strftime("%-m/%-d") for i in range(report_periods)]
forecast_dates =[(start_datetime + timedelta(days=i)).strftime("%-m/%-d") for i in range(forecast_periods)]
fit_start = report_dates.index(fit_period[0])
fit_end = report_dates.index(fit_period[1])
#E,Wはわからないので、13日後、8日後の感染者数とする。
E_0=covid_data["pcr_tested_positive"].iloc[fit_start+13]
W_0=covid_data["pcr_tested_positive"].iloc[fit_start+8]
I_0=covid_data["pcr_tested_positive"].iloc[fit_start]-covid_data["discharged"].iloc[fit_start]-covid_data["death"].iloc[fit_start]
R_0=covid_data["discharged"].iloc[fit_start]
F_0=covid_data["death"].iloc[fit_start]
#学習する。
model = SEWIRF_estimator([E_0,W_0,I_0,R_0,F_0],ratio)
model.fit(covid_data["pcr_tested_positive"].values[fit_start:fit_end+1],covid_data["death"].values[fit_start:fit_end+1])
print(f"感受性者保持者:{model.S_0:,.0f}人")
print(f"再生産数({report_dates[fit_start]}起点):{model.R0:.2f}")
print(f"回復期間:{model.recover_date:.0f}日")
print(f"潜伏期間:{model.latent_date:.0f}日")
print(f"報告待期間:{model.judge_date:.0f}日")
print(f"致死率:{model.mortal_rate*100:.2f}%")
#RMSE
params = model.S_0,model.R0,model.recover_date,model.latent_date,model.judge_date,model.mortal_rate
rmse_confirmed,rmse_deaths = model.rmse(params,
covid_data["pcr_tested_positive"].values[fit_start:fit_end+1],
covid_data["death"].values[fit_start:fit_end+1])
print(f"学習期間RMSE(感染者数):{rmse_confirmed:,.0f}人")
print(f"学習期間RMSE(死者数):{rmse_deaths:,.0f}人")
if fit_end + 1 < report_periods:
rmse_confirmed,rmse_deaths = model.rmse(params,
covid_data["pcr_tested_positive"].values[fit_end+1:],
covid_data["death"].values[fit_end+1:],
fit_end+1-fit_start)
print(f"検証期間RMSE(感染者数):{rmse_confirmed:,.0f}人")
print(f"検証期間RMSE(死者数):{rmse_deaths:,.0f}人")
#予測する。
result = model.predict(forecast_periods-fit_start)
confirmed_total = np.concatenate([[None] * fit_start , result.y[3] + result.y[4] + result.y[5]])
death_total = np.concatenate([[None] * fit_start , result.y[5]])
#日毎のデータ算出
confirmed_daily = np.concatenate([[None] * fit_start , np.diff(result.y[3] + result.y[4] + result.y[5])])
death_daily = np.concatenate([[None] * fit_start , np.diff(result.y[5])])
confirmed_daily_report = covid_data["pcr_tested_positive"].diff()[1:]
death_daily_report = covid_data["death"].diff()[1:]
confirmed_daily_report_ma = confirmed_daily_report.rolling(7,min_periods=1,center=True).mean()
death_daily_report_ma = death_daily_report.rolling(7,min_periods=1,center=True).mean()
fig = plt.figure(figsize=(16, 12))
for i in range(1,5):
ax = fig.add_subplot(2,2,i)
if i % 2 == 0:
type = "新規"
start_x = 1
else:
type = "累計"
start_x = 0
if i <= 2:
data_label = f"感染者数({type})"
else:
data_label = f"死亡者数({type})"
if i==1:
#感染者数（累計）
data_predict = confirmed_total
data_report = covid_data["pcr_tested_positive"]
data_report_ma = None
elif i==2:
#感染者数（新規）
data_predict = confirmed_daily
data_report = confirmed_daily_report
data_report_ma = confirmed_daily_report_ma
elif i==3:
#死亡者数（累計）
data_predict = death_total
data_report = covid_data["death"]
data_report_ma = None
elif i==4:
#死亡者数（新規）
data_predict = death_daily
data_report = death_daily_report
data_report_ma = death_daily_report_ma
ax.set_title(f"SEWIR-Fモデル {data_label}", fontsize=16)
ax.set_xlabel("日付",fontsize=15)
ax.set_ylabel("人数",fontsize=15)
ax.set_xticks(np.arange(0,forecast_periods,15))
#予測値
ax.plot(forecast_dates[start_x:],data_predict,label="予測値")
ax.annotate("{:,.0f}".format(data_predict[-1]), xy = (forecast_dates[-1], data_predict[-1]),fontsize=10)
ax.annotate("{:,.0f}".format(data_predict[report_periods-1]), xy = (report_dates[-1], data_predict[report_periods-1]),fontsize=10)
#報告値
ax.plot(report_dates[start_x:],data_report,label="報告値",ls="--")
ax.annotate("{:,.0f}".format(data_report.iloc[-1]),xy = (report_dates[-1], (data_report.iloc[-1])),fontsize=10)
if data_report_ma is not None:
ax.plot(data_report_ma,label="報告値(移動平均)")
#学習期間
ax.axvspan(fit_start, fit_end, color="lightblue", alpha=0.3, label="学習期間")
#検証期間
if fit_end + 1 < report_periods:
ax.axvspan(fit_end+1, report_periods-1, color="lightgreen", alpha=0.3, label="検証期間")
ax.legend(fontsize=10)
plt.savefig(f"./SEWIRF_estimate_{file_suffix}.png",bbox_inches='tight', pad_inches=0.2)
plt.show()
なお後々のために学習（フィット）させるデータの期間を指定できるようにしております。
全データで学習した場合(5/18まで）
まずは全データ(2/5-5/18)を学習に使用して100日後までの感染状況を予測してみましょう。
呼び出すためのコードは以下となります。
plot_SEWIRF_predicted(covid_data,("2/5","5/18"),"fit_all",forecast_day=100)
結果は以下の通りです。
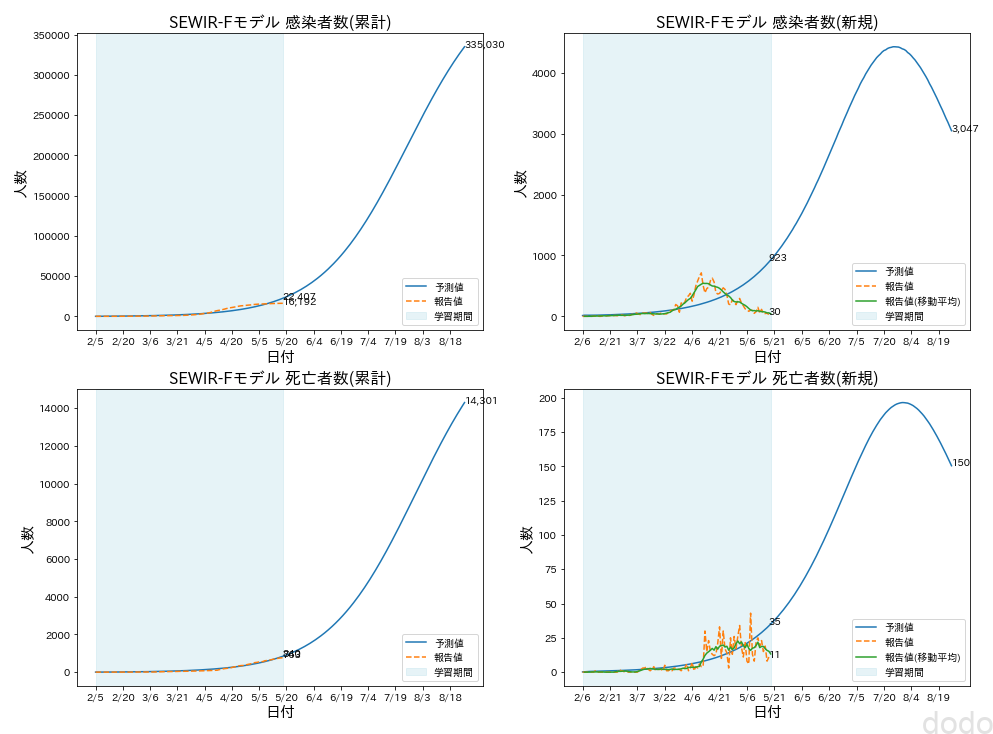SEWIRFモデル予想（学習データ：2/5-5/18)学習データで最適化されたパラメータとRMSE（二乗平均平方根誤差）は以下になります。
- 感受性者保持者:1,000,000人
- 再生産数(2/5起点):0.80
- 回復期間:5日
- 潜伏期間:1日
- 報告待期間:3日
- 致死率:4.48%
- 学習期間RMSE(感染者数):2,081人
- 学習期間RMSE(死者数):34人
RMSEとグラフを見るとわかりますが、すでに学習データ自身がうまくフィットしていません。特に４月以降は実データが収束に向かっているのに対して、モデルでは拡大に向かっています。
２月のデータで学習した場合
全データで学習するのをやめて、２月のデータで学習して、３月以降のデータで検証してみます。
コードは以下となります。
plot_SEWIRF_predicted(covid_data,("2/5","2/29"),"fit_feb",forecast_day=100)
結果は以下の通りです。
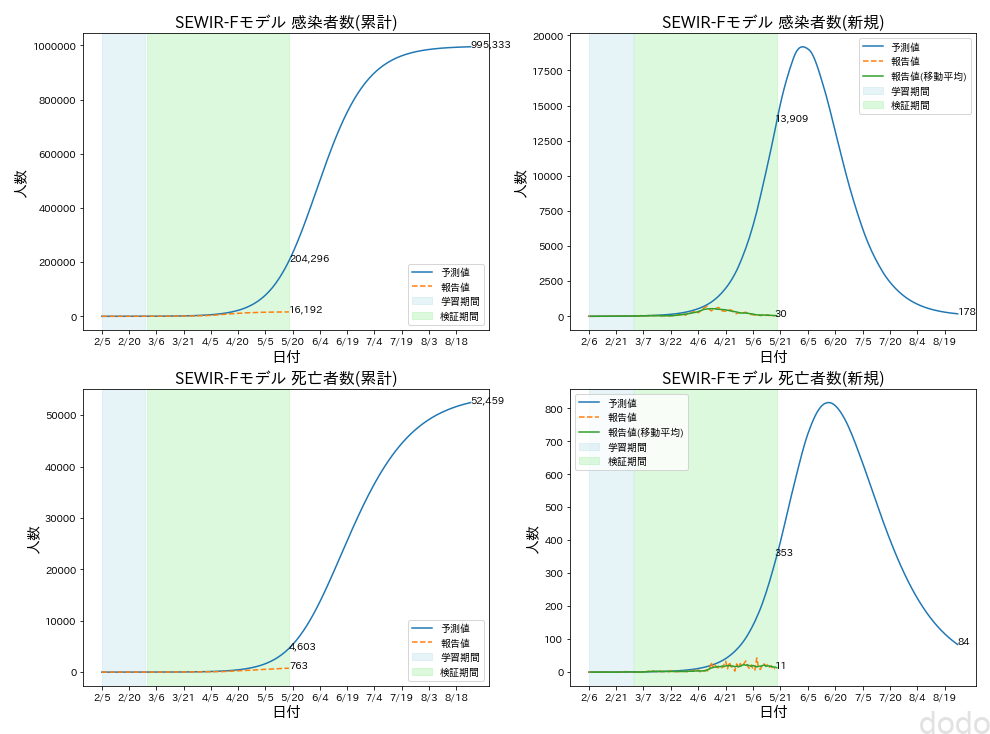SEWIRFモデル予想（学習データ：2/5-2/29)学習データで最適化されたパラメータとRMSEは以下になります。
- 感受性者保持者:1,000,000人
- 再生産数(2/5起点):4.00
- 回復期間:20日
- 潜伏期間:10日
- 報告待期間:10日
- 致死率:5.43%
- 学習期間RMSE(感染者数):12人
- 学習期間RMSE(死者数):1人
- 検証期間RMSE(感染者数):54,223人
- 検証期間RMSE(死者数):1,043人
RMSE、グラフを見れば一目瞭然ですが、４月以降のデータに対して全く予測が出来ていません。
3月のデータで学習した場合
次に３月のデータで学習し、４月以降のデータで検証します。
コードは以下となります。
plot_SEWIRF_predicted(covid_data,("3/1","3/31"),"fit_mar",forecast_day=100)
結果は以下の通りです。
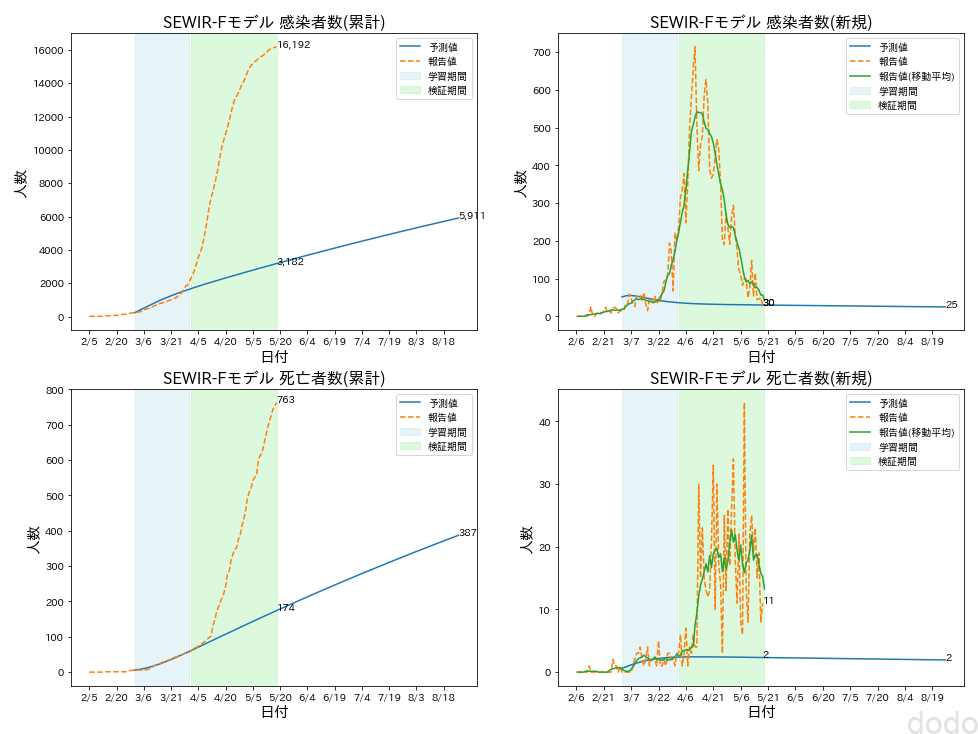SEWIRFモデル予想（学習データ：3/1-3/31)学習したデータで最適化されたパラメータとRMSEは以下になります。
- 感受性者保持者:1,000,000人
- 再生産数(3/1起点):0.68
- 回復期間:30日
- 潜伏期間:10日
- 報告待期間:10日
- 致死率:7.41%
- 学習期間RMSE(感染者数):194人
- 学習期間RMSE(死者数):2人
- 検証期間RMSE(感染者数):9,653人
- 検証期間RMSE(死者数):311人
学習データには良くフィットしてますが、４月以降のデータの予測は完全に外れています。
4月のデータで学習した場合
次に4月のデータで学習し、5月以降のデータで検証します。
コードは以下となります。
plot_SEWIRF_predicted(covid_data,("4/1","4/30"),"fit_apr",forecast_day=100)
結果は以下の通りです。
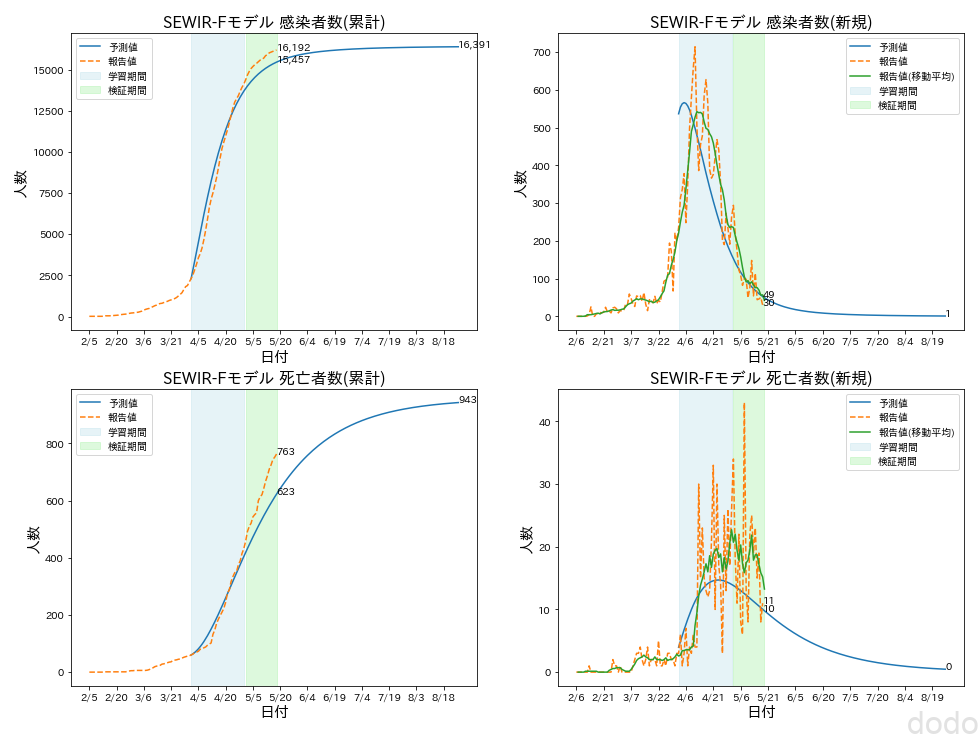SEWIRFモデル予想（学習データ：4/1-4/30)学習したデータで最適化されたパラメータとRMSEは以下になります。
- 感受性者保持者:1,000,000人
- 再生産数(4/1起点):0.04
- 回復期間:30日
- 潜伏期間:10日
- 報告待期間:10日
- 致死率:5.65%
- 学習期間RMSE(感染者数):839人
- 学習期間RMSE(死者数):21人
- 検証期間RMSE(感染者数):740人
- 検証期間RMSE(死者数):99人
RMSEを見ると学習データ、検証データともに少ない誤差に抑えられているのがわかります。またグラフ上も比較的、良くフィットしているのがわかります。
４月初旬（感染のタイムラグを考えると３月初旬から中旬）からデータの傾向が変わってる事は可視化した段階でわかりますが、その変化がSEWIR-Fモデルで吸収できる変化でなく、外的な要因にある事が推定できます。
なおデータのフィッティングは悪くないですが、4月1日の再生産数が0.04というのがちょっと小さすぎます。
潜伏期間、回復期間も報告されている数値より大きい値となっているので、パラメータの釣り合いで局所最小値に陥っている可能性も否定できません。
4月以降の全データで学習した場合(5/18まで）
検証は出来ませんが、最後に４月以降のデータ全てで学習した場合に100日後までを予測します。
コードは以下となります。
plot_SEWIRF_predicted(covid_data,("4/1","5/18"),"fit_apr_may",forecast_day=100)
結果は以下の通りです。
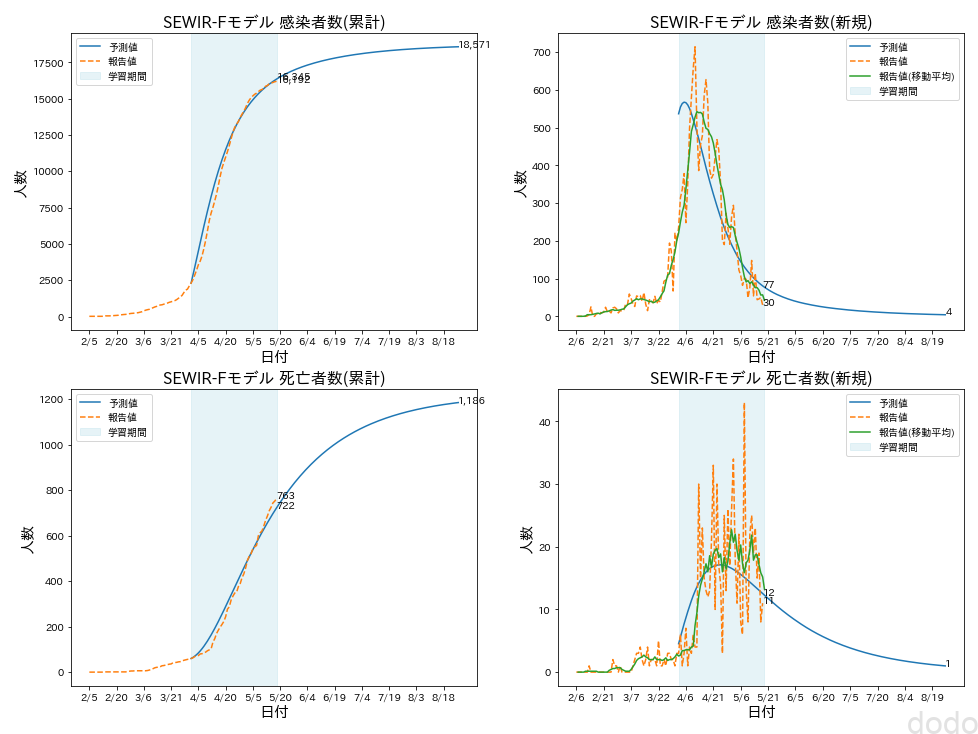SEWIRFモデル予想（学習データ：4/1-5/18)学習したデータで最適化されたパラメータとRMSEは以下になります。
- 感受性者保持者:1,000,000人
- 再生産数(4/1起点):0.13
- 回復期間:30日
- 潜伏期間:10日
- 報告待期間:10日
- 致死率:6.40%
- 学習期間RMSE(感染者数):684人
- 学習期間RMSE(死者数):31人
再生産数は、４月のデータのみで学習した場合よりも現実的にありそうな値になっています。また学習に使ったので当たり前ですが、５月のデータにも良くフィットしています。
実際の検証は未来にならないと出来ませんが、現在の傾向が続けば、６月頃にはほぼ収束している事になります。
再流行の可能性を除外すれば（除外できないと思いますが・・）、最終的な感染者数は約20,000人、死亡者数は1,000人程度といったところでしょうか・・
考察
予測の計算をする上で注意する必要があると思ったのは以下の２点です。
① 外的要因、介入で傾向が変わった場合は予測がうまく行かない。
２月、３月のデータを学習に使用すると予測がうまく行かない事から４月のデータからSIRモデルで吸収できないような変化が発生している事が考えられます。
つまり何かしらの介入（自粛による接触減、季節性、外部（つまり外国）との人の交流など）があった場合、SIRモデルのパラメータの修正が必要になります。
② 非線形の最適化手法で決定されたパラメータの解釈は注意が必要。
非線形の最適化手法の場合、局所最小値におちいりやすい傾向があります。
記事内では示しませんでしたが、非現実的なパラメータでも変な組み合わせで割とフィットしてしまう現象がちょくちょく発生しました。
実装上でのパラメータの初期値と範囲の指定は注意が必要です。（「SEWIRF_estimator」クラスのの「fit」メソッドで実装しています。）
なのでパラメータの釣り合いでたまたま、データにうまくフィットしているだけかもしれないので、パラメータ個々の信憑性（再生産数、致死率、回復期間など）は若干、怪しいかと思います。（本気で分析するなら、さらなる考察が必要になるでしょう。）
まとめ
以上、新型コロナにて、SIRモデル（SEWIR-Fモデル）にて実データからパラメータを決定して未来の感染状況の予測をする事を試みました。
ただ、考察で記載したように何かしらの外的要因が発生すれば、予測は大幅にずれます。
（2020/9/16追記 そして第二波が来たので外れました・・）
それを考えるとこのような感染症の予測問題というのは、やはり難しいという印象です。
