Coursera「機械学習」の2週目では、「重回帰」について説明しており、また実際に使用する場合に必要な事として、特徴量のスケーリング、学習率の調整、そして多項式回帰について記載しています。
また最急降下法ではなく、解析的に問題を解く場合の方法として正規方程式を使う方法についてもちらっと説明されてます。
本記事では、上記についての概要と所感について記載していきます。
なお、2週目の後半のOctaveのチュートリアルについては割愛します・・(需要もないと思うので・・)
重回帰
単回帰は、「家の広さ」から「家の販売価格」を予測するなど、一つの特徴量\(x\)からある値\(y\)を予測するモデルでしたが、重回帰は、複数の特徴量・・例えば「家の広さ」\(x_1\)、「家の間取り」\(x_2\)、「家の建築年数」\(x_3\)、「場所」\(x_4\)・・などから、ある値、「家の販売価格」\(y\)を予測するモデルです。
数式で表すとモデルは以下のようになります。(nは特徴量の数)
$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n$$
以後、行列表現をすることによって、式がスッキリします。
ここで表現の統一性と計算の簡略化のために\(m\)を教師データの数、\(x^{(i)}\)はそれぞれのデータの変数の値として、以下のような常に値が1となるダミー的な変数として\(x_0^{(i)}\)を定義します。
$$x_0^{(i)} = 1 \;(\text{for } i=0\dots m ) $$
さらに以下のように\(x\)と\(\theta\)の行列を定義します。
\begin{align}
x&=\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n \end{bmatrix} \\
\theta&=\begin{bmatrix} \theta_0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}
\end{align}
すると式(1)は以下のように表す事ができます。
$$h_\theta(x)=\theta^Tx$$
後は単回帰の場合と同じように、目的関数と \(\theta\)を求めるための最急降下法のルールを導出すれば良いわけです。
ここでさらに以下のような\(X\)と\(\vec{y}\)を定義します。
\begin{align}
X &= \begin{bmatrix} x_0^{(1)} & x_1^{(1)} & \ldots & x_n^{(1)} \\ x_0^{(2)} & x_1^{(2)} & \ldots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots \\ x_0^{(m)} & x_1^{(m)} & \ldots & x_n^{(m)} \end{bmatrix}\\
\vec{y}&=\begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix}
\end{align}
細かい計算は省略しますが、以上から目的関数は以下の式で表現できます。
$$J(\theta)=\frac{1}{2m}(X\theta-\vec{y})^{T}(X\theta-\vec{y})$$
そして目的関数の微分は以下のようになります。
$$\nabla J(\theta)=\frac{1}{m}X^{T}(X\theta-\vec{y})$$
よって最急降下法のルールも以下で表現でき、\(\theta\)を求める事ができます。
$$\theta:=\theta-\alpha \frac{1}{m}X^{T}(X\theta-\vec{y})$$
正規化
ここから少し実践的な話になります。
「販売価格」を求めるための変数となる「家の広さ」、「家の間取り」、「家の建築年数」などは、単位が異なるので、ある値は0から1000000くらいの値になるし、ある値は0から10くらいの値にしかならないかもしれません。
このように、変数による大きさが違いすぎると最急降下法の繰り返し実行が収束しにくくなルため、以下のような正規化(normalization)というものを実行します。
$$x_i:=\frac{x_i-\mu_i}{s_i}$$
ここで\(\mu_i\)は変数\(x_i\)の各値の平均、\(s_i\)は\(x_i\)の値の最大値と最小値の差分、もしくは標準偏差とします。
これによって各値はだいたい-1から1の間の範囲内になるため最急降下法の計算がしやすくなります。
学習率
最急降下法において、学習率\(\alpha\)は「いい具合」な値を選ぶわけですが、それが「いい具合」な値になっているかを検証する方法について言及されてます。
結論から言いますと、最急降下法の実施回数と目的関数の値をプロットしてちゃんと収束していってるかどうか確かめましょうということです。
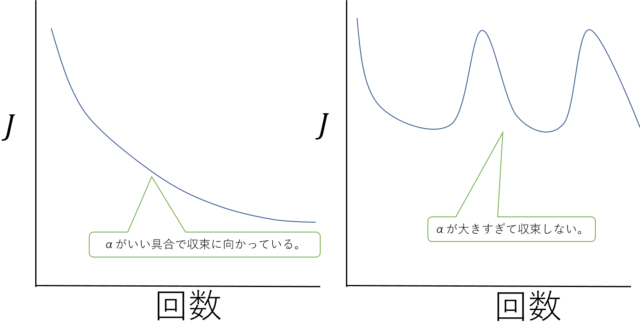 目的関数と学習率(左は収束しているが右は収束していない)
目的関数と学習率(左は収束しているが右は収束していない)学習率が大きすぎると小さくなっていかないし、逆に小さすぎると収束が遅くなります。
ここは正直、まあ、そりゃそうだよな・・と思いました。
後は、じゃあ「収束ってどの程度になったら収束やねん」てことですが、だいたい求めた目的関数の差が\(10^{-3}\)以下になったぐらいだとの事です。
ただ、これも実際には明確に決めるのは難しいと言ってます。
多項式回帰
ここまでは、変数\(x\)と\(y\)の関係が線形であることを前提にモデルを作って来ましたが、以下の図のケースのように線形でないほう(左図よりも右図)の方がよりデータにフィットする場合もあります。
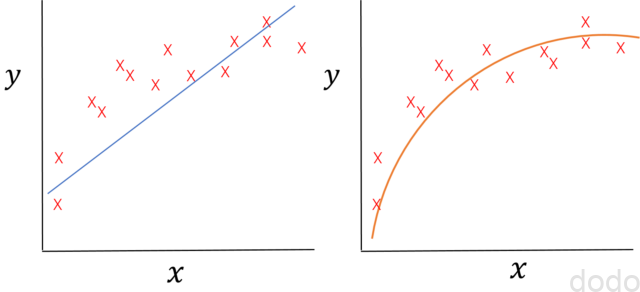 データのフィッティングの比較(右のほうがよりフィットしている。)
データのフィッティングの比較(右のほうがよりフィットしている。)数式で表すと・・
$$h_\theta(x)=\theta_0+\theta_1x$$
とするよりも・・
$$h_\theta(x)=\theta_0+\theta_1x+\theta_2\sqrt{x}$$
などとしたほうがより良くフィットする事になります。
データによっては、
$$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^{2}+\theta_2x^{3}$$
などとしたほうが良い場合もあるかと思います。
こういう場合は、私はもう線形回帰では計算できないものだと思ってました。
でも結局、例えば\(x_2=\sqrt{x}\)のように新しい特徴量を定義すれば、式(13)は、
$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2$$
のようになるので、教師データとしてもあらかじめ「家の広さ」(\(x_1\))というデータがあれば、「\(\sqrt{\text{家の広さ}}\)」(\(x_2\))を計算して違う特徴量として用意すればいいわけです。
ただ実践的には、どういう特徴量を用意すれば良いのかという問題があります。
上のようにプロットして見た目で想像がつく場合は良いですが、通常は、\(\sqrt{x}\)を選ぶか\(x^2\)を選ぶか\(x^3\)を選べば良いかわからないし、さらに特徴量が複数の場合は、\(x_1x_2\)や\(x_1x_2^2\)など組み合わせが途方もない数になり、どれを変数として追加すれば良いか簡単にはわかりません。
この問題についてはこの後の週の講義でどうすれば良いか言及されております。
なおこのように既存の特徴量から新しい特徴量を作る場合は、より「正規化」が重要になります。二乗だの三乗だのしたら、それこそスケールが大きく変わってくるので・・
正規方程式
前回の記事でもちょこっと触れましたが、目的関数を微分できるので、最急降下法とか使わなくても解析的な方法で\(\theta\)を求める事ができます。
計算は省略しますが、求める式は以下のようになります。
$$\theta=(X^{T}X)^{-1}X^{T}\vec{y}$$
最急降下法と異なり、学習率\(\alpha\)をいい具合に決める必要もなければ、何度も計算を繰り返す必要もありません。
じゃあ、なんで最急降下法とか使うのかと言うと、変数の数が多い時(講座では10,000を超えたあたり)から計算のコストが非常に大きくなるからです。
具体的には\((X^{T}X)\)の計算コストが莫大に跳ね上がります。
なので、実際のデータによってケースバイケースで使い分けるイメージでしょうか・・
後は、\((X^{T}X)\)の逆行列が求められないケースとし以下のケースがあります。
- 変数同士の相関が強い場合
- 教師データ数(\(m\))よりも特徴量の数(\(n\))の方が大きい場合
この場合は、Octaveのでは、単純な逆行列ではなく、一般化逆行列のライブラリを使えば、うまいようにやってくれる(逆行列は求められなくても一般化逆行列は求められる。)との事で、あまり深くは追求されてません。
まとめ
2週目からOctaveによる実践が始まりますが、関数の中身を埋めていくだけなので、上述にあるような数式がわかれば、楽勝でした。
まだいわゆる一般の人がイメージするAIとか機械学習といった感じではないですが、やっぱり基本は大事だなと思います。
基本的な事がわかってないと、お客さんとの会話でもちょっとした時にボロが出るんですよね・・
次回は、第3週目となるロジスティック回帰についての受講記を書きます。