本記事では、Coursera機械学習の第3週の後半で説明されている「正則化」についてまとめていきます。
因みに第2週で出てきた正規化(normalization)と、ここで扱う正則化(regularization)は全く違う概念なので、要注意です。（日本語訳が悪いと思う・・）
過学習
教師あり学習で注意しなくてはいけない事の一つに「過学習」があります。
まずは回帰の例を以下の図で見てみましょう。
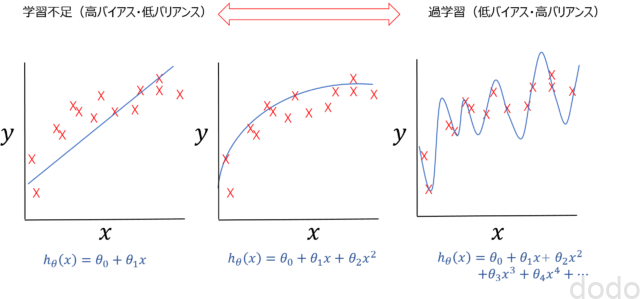過学習のイメージ（回帰）上の３つのグラフの中で一番左の図は単純に特徴量で回帰した場合のイメージ、真ん中が特徴量の２次の項を追加した場合のイメージ（２次曲線の形はちょっと違うけどまあ、そこは勘弁してください・・）、一番右の図が高次の項をたくさん追加したもののイメージです。
この中では、右のグラフが最もデータにフィットした曲線になっていますが、ではそれが最も良いモデルと言えるでしょうか！？
波形が山・谷になっている所を見ると想像がつくかと思いますが、右のモデルは教師データには完全にフィットしてますが、新しいデータに対しては、あまりよく機能しません。
このようなモデルの状態を「過学習」と言います。
また別の言い方では「低バイアス」「高バリアンス」の状態と言います。（逆に左のモデルは「高バイアス」「低バリアンス」の状態）
バイアス・バリアンスがちょうど良く、適度な学習をしているのは、真ん中のグラフのモデルです。
分類でも同様です。
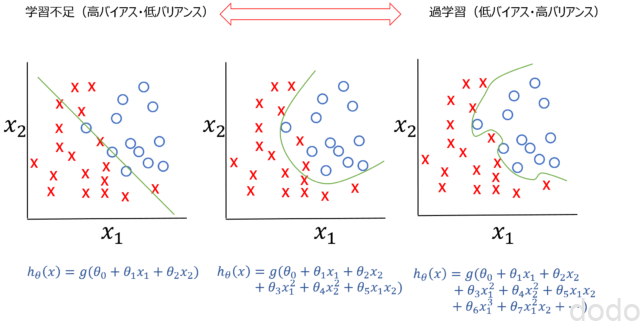過学習のイメージ（分類）右に行くほど高次の特徴量を追加してますが、一番、右のグラフは過学習している状態となり、ちょうど良いのは、真ん中のグラフのモデルになります。
なお、上の例ではある特徴量の高次の次数を増やしていきましたが、例えば家の販売価格を予測するために、家の広さ・部屋の数・建築年数・ベッドの数・庭の広さ・・などと別の特徴量を増やしていっても同じ現象が発生します。
因みに過学習は英語では「over-fitting」と言います。逆の状態は、英語で「under-fitting」と言うのですが、これに該当する日本語が「未学習」「未適合」など人によって曖昧で、バシッとしたものがありません。また全く学習してないわけじゃいので未学習ってのはちょっと違うんじゃないかな・・と個人的に思ったりします。なので図内では、独断で「under-fitting」を学習不足と書きました。
正則化
では、うまい具合に特徴量を含めたモデルを作るにはどうすれば良いのでしょうか？
自分で、どの特徴量を追加するか調整する方法もありますが、いろんな特徴量を入れたままで、いい具合に調整してくれる手法として「正則化」という方法があります。
例として以下のようなモデルを考えてみましょう。
$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4$$
この場合、以下の目的関数・・
$$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$
を以下のように変更したら一体何が起きるでしょうか？
$$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+1000\cdot\theta_3^2+1000\cdot\theta_4^2$$
上式に対して、最急降下法などを使って目的関数を最小にしようとすると、\(\theta_3\)、\(\theta_4\)の係数が大きいため、相対的に\(\theta_3\)、\(\theta_4\)が小さくなります。（つまり\(x_3\)、\(x_4\)の寄与が小さくなります。）
つまり、寄与を少なくするためには何かしら\(\theta_j^2\)に大きい係数をかけた項を追加すれば良いわけです。
ただ最初から、どの特徴量の寄与を少なくしたいかは、わかりません。
よって、以下のように全ての\(\theta_j^2\)（\(\theta_0^2\)を除く）についての項を加えたものを目的関数とします。
$$J(\theta)=\frac{1}{2m}[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2]$$
全部の\(\theta_j^2\)に同じ係数をかけているから「全部の寄与が小さくなるだけじゃないの？」と思ってしまいますが、これがうまい事に、計算すると特徴量ごとの寄与を上手く調整してくれます。
ただし、パラメータの\(\lambda\)は自分で決める必要があります。
\(\lambda\)が小さ過ぎると正則化していないのと同じだし、\(\lambda\)が大き過ぎるとどの特徴量の寄与もない状態になってしまうので、良い具合に選ぶ必要があります。
以下、本講座の演習のプログラムで\(\lambda\)を0,1,10,100と変える事によって、分類問題の決定境界がどのように変わるかを試した結果です。
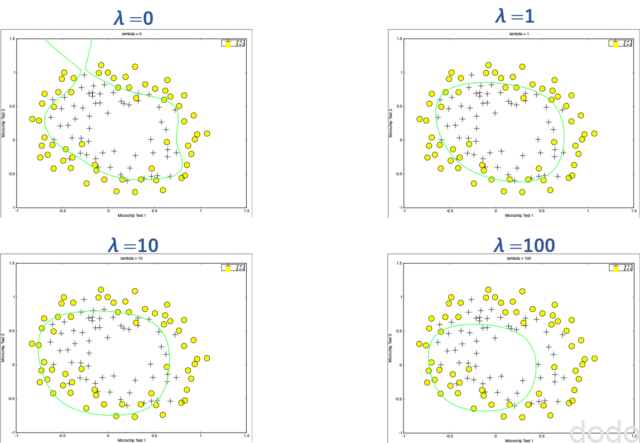正則化の例\(\lambda=0\)だと、正則化してないため過学習しており、\(\lambda=100\)だと学習不足になってしまっているのがわかると思います。
以上から、式を整理して行列で表現すると線形回帰、ロジスティック回帰の場合のそれぞれの目的関数とその偏微分は以下のようになります。（\(X\)や\(\theta\)などの行列の定義は第2週の受講記と同様です。）
線形回数の場合
\begin{eqnarray}J(\theta)&=&\frac{1}{2m}[(X\theta-y)^{T}(X\theta-y)+\lambda\cdot(L\theta)^T(L\theta) ]\\
\nabla J(\theta)&=&\frac{1}{m}[X^{T}(X\theta-y)+\lambda\cdot (L\theta)] \end{eqnarray}
ロジスティック回帰の場合
\begin{eqnarray}J(\theta)&=&\frac{1}{m}[\left(-y^{T}\log(g(X\theta))-(1-y)^{T}\log(1-g(X\theta))\right)+\frac{1}{2}\lambda\cdot (L\theta)^T(L\theta)]\\\nabla J(\theta)&=&\frac{1}{m}[X^{T}(g(X\theta)-y)+\lambda\cdot (L\theta)]\end{eqnarray}
ここで上の式に含まれる\(L\)は以下で定義されるものとします。(\(\theta_0\)は正則化しないため、このように定義しています。）
$$L = \begin{bmatrix} 0 & & & & \newline & 1 & & & \newline & & 1 & & \newline & & & \ddots & \newline & & & & 1 \newline\end{bmatrix}$$
これらの式から最急降下法やBFGS法で\(\theta\)を求める事ができます。
正規方程式
講座では正則化した場合の正規方程式についても言及されてます。
第2週目であったように特徴量の数が少ない場合（10,000未満）ならば現実的にも正規方程式を使って解く事ができるのですが、正則化項を入れた場合の正規方程式は以下のようになります。
$$\theta = \left( X^TX + \lambda \cdot L \right)^{-1} X^Ty$$
\(L\)の定義は式(9)と同様です。
第2週目の受講記で述べたように特徴量の数がデータの数よりも大きくなると、\(X^TX\)の逆行列が存在しませんが、正則化項を入れた場合は、\(X^TX+ \lambda \cdot L\)に逆行列が存在し計算できるようになります。
まとめ
Coursera機械学習の第3週の後半の正則化についてまとめました。
正則化項を導入する意義や、「何故導入すると寄与が小さくなるのか」の直感的な説明はわかりやすかったと思います。
ただ、講座で説明されているのは、正則化として目的関数に\(\theta\)を二乗した項を付与する方法（リッジ回帰）ですが、実は他にも\(\theta\)の絶対値を追加する方法（ラッソ回帰）もあります。（２つを混ぜ合わせて使う方法もあります。）
この講座では、時間の都合上か、何かしらのポリシーだかわかりませんが、リッジ回帰しか扱ってません。
他を全く知らないと「正則化＝\(\theta\)を二乗した項を追加」との誤解を与えるので、扱わないまでもちょっとくらい言及されても良いのではと思いました。
次は、いよいよ第四週のニューラルネットワークについてまとめていきたいと思います。
